EDP Sciences logo
Subscriber Authentication Point
Search
Menu
All issues Volume 11 / No 2 (April 2005) ESAIM: COCV, 11 2 (2005) 204-218 References
Free Access
Issue
ESAIM: COCV
Volume 11, Number 2, April 2005
Page(s) 204 - 218
DOI https://doi.org/10.1051/cocv:2005002
Published online 15 March 2005
  1. M. Abdelouhab, J.L. Bona, M. Felland and J.-C. Saut, Nonlocal models for nonlinear, dispersive waves. Physica D 40 (1989) 360–392. [CrossRef] [MathSciNet] [Google Scholar]
  2. M.J. Ablowitz and A.S. Fokas, The inverse scattering transform for the Benjamin-Ono equation-a pivot to multidimensional problems. Stud. Appl. Math. 68 (1983) 1–10. [MathSciNet] [Google Scholar]
  3. T.B. Benjamin, Internal waves of permanent form in fluids of great depth. J. Fluid Mech. 29 (1967) 559–592. [CrossRef] [Google Scholar]
  4. J. Bona and R. Winther, The Korteweg-de Vries equation, posed in a quarter-plane. SIAM J. Math. Anal. 14 (1983) 1056–1106. [CrossRef] [MathSciNet] [Google Scholar]
  5. J. Bourgain, Fourier transform restriction phenomena for certain lattice subsets and applications to nonlinear evolution equations. Geom. Funct. Anal. 3 (1993) 107–156, 209–262. [CrossRef] [MathSciNet] [Google Scholar]
  6. K.M. Case, Benjamin-Ono related equations and their solutions. Proc. Nat. Acad. Sci. USA 76 (1979) 1–3. [CrossRef] [Google Scholar]
  7. T. Cazenave and A. Haraux, An Introduction to Semilinear Evolution Equation. Oxford Sci. Publ. (1998). [Google Scholar]
  8. J. Colliander and C.E. Kenig, The generalized Korteweg-de Vries equation on the half line. Comm. Partial Differential Equations 27 (2002) 2187–2266. [Google Scholar]
  9. K.D. Danov and M.S. Ruderman, Nonlinear waves on shallow water in the presence of a horizontal magnetic field. Fluid Dynamics 18 (1983) 751–756. [CrossRef] [MathSciNet] [Google Scholar]
  10. A.E. Ingham, A further note on trigonometrical inequalities. Proc. Cambridge Philos. Soc. 46 (1950) 535–537. [CrossRef] [MathSciNet] [Google Scholar]
  11. R. Iorio, On the Cauchy problem for the Benjamin-Ono equation. Comm. Partial Differentiel Equations 11 (1986) 1031–1081. [CrossRef] [Google Scholar]
  12. Y. Ishimori, Solitons in a one-dimensional Lennard/Mhy Jones lattice. Progr. Theoret. Phys. 68 (1982) 402–410. [Google Scholar]
  13. C.E. Kenig and K. Koenig, On the local well-posedness of the Benjamin-Ono and modified Benjamin-Ono equations. Math. Res. Lett. 10 (2003) 879–895. [MathSciNet] [Google Scholar]
  14. C.E. Kenig, G. Ponce and L. Vega, A bilinear estimate with application to the KdV equation. J. Amer. Math Soc. 9 (1996) 573–603. [Google Scholar]
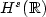  15. H. Koch and N. Tzvetkov, On the local well-posedness of the Benjamin-Ono equation in Formula . Int. Math. Res. Not. 26 (2003) 1449–1464. [CrossRef] [Google Scholar]
  16. Y. Matsuno and D.J. Kaup, Initial value problem of the linearized Benjamin-Ono equation and its applications. J. Math. Phys. 38 (1997) 5198–5224. [CrossRef] [MathSciNet] [Google Scholar]
  17. S. Micu, On the controllability of the linearized Benjamin-Bona-Mahony equation. SIAM J. Control Optim. 39 (2001) 1677–1696. [CrossRef] [MathSciNet] [Google Scholar]
  18. H. Ono, Algebraic solitary waves in stratified fluids. J. Phys. Soc. Japan 39 (1975) 1082–1091. [Google Scholar]
  19. A. Pazy. Semigroups of linear operators and applications to partial differential equations. Springer-Verlag, New York, Appl. Math. Sci. 44 (1983). [Google Scholar]
  20. G. Perla-Menzala, F. Vasconcellos and E. Zuazua. Stabilization of the Korteweg-de Vries equation with localized damping. Quart. Appl. Math. 60 (2002) 111–129. [MathSciNet] [Google Scholar]
  21. G. Ponce, On the global well-posedness of the Benjamin-Ono equation. Diff. Integral Equations 4 (1991) 527–542. [Google Scholar]
  22. L. Rosier, Exact boundary controllability for the Korteweg-de Vries equation on a bounded domain. ESAIM: COCV 2 (1997) 33–55. [CrossRef] [EDP Sciences] [Google Scholar]
  23. D.L. Russell and B.-Y. Zhang, Controllability and stabilizability of the third order linear dispersion equation on a periodic domain. SIAM J. Cont. Optim. 31 (1993) 659–676. [CrossRef] [Google Scholar]
  24. D.L. Russell and B.-Y. Zhang, Exact controllability and stabilizability of the Korteweg-de Vries equation. Trans. Amer. Math. Soc. 348 (1996) 3643–3672. [CrossRef] [MathSciNet] [Google Scholar]
  25. T. Tao, Global well-posedness of the Benjamin-Ono equation in 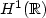Formula , preprint (2003). [Google Scholar]

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.