| Issue |
ESAIM: COCV
Volume 15, Number 3, July-September 2009
|
|
|---|---|---|
| Page(s) | 712 - 740 | |
| DOI | https://doi.org/10.1051/cocv:2008044 | |
| Published online | 19 July 2008 | |
Nonlinear diffusion equations with variable coefficients as gradient flows in Wasserstein spaces
Dipartimento di Scienze e Tecnologie Avanzate,
Università degli Studi del Piemonte Orientale, Italy. stefano.lisini@unipv.it
Received:
15
May
2007
Revised:
4
February
2008
We study existence and approximation of non-negative solutions of partial differential equations of the type
 where A is a symmetric matrix-valued function of the spatial variable satisfying a uniform ellipticity condition,
where A is a symmetric matrix-valued function of the spatial variable satisfying a uniform ellipticity condition,
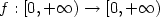 is a suitable non decreasing function,
is a suitable non decreasing function, 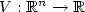 is a convex function.
Introducing the energy functional
is a convex function.
Introducing the energy functional 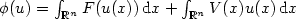 ,
where F is a convex function linked to f by
,
where F is a convex function linked to f by 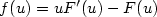 ,
we show that u is the “gradient flow” of ϕ with respect to the
2-Wasserstein distance between probability measures on
the space
,
we show that u is the “gradient flow” of ϕ with respect to the
2-Wasserstein distance between probability measures on
the space 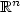 , endowed with the Riemannian distance induced by
, endowed with the Riemannian distance induced by 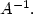 In the case of uniform convexity of V, long time asymptotic behaviour and decay rate to the stationary state
for solutions of equation (0.1) are studied.
A contraction property in Wasserstein distance for solutions of equation (0.1)
is also studied in a particular case.
In the case of uniform convexity of V, long time asymptotic behaviour and decay rate to the stationary state
for solutions of equation (0.1) are studied.
A contraction property in Wasserstein distance for solutions of equation (0.1)
is also studied in a particular case.
Mathematics Subject Classification: 35K55 / 35K15 / 35B40
Key words: Nonlinear diffusion equations / parabolic equations / variable coefficient parabolic equations / gradient flows / Wasserstein distance / asymptotic behaviour
© EDP Sciences, SMAI, 2008
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


