| Issue |
ESAIM: COCV
Volume 14, Number 1, January-March 2008
|
|
|---|---|---|
| Page(s) | 148 - 159 | |
| DOI | https://doi.org/10.1051/cocv:2007050 | |
| Published online | 21 September 2007 | |
Curl bounds Grad on SO(3)
1
Department of Mathematics, Technische Universität Darmstadt, Schlossgartenstrasse 7, 64289 Darmstadt, Germany; neff@mathematik.tu-darmstadt.de
2
Institut für Baustatik, Universität Karlsruhe (TH), Kaiserstrasse 12, 76131 Karlsruhe, Germany; im@bs.uka.de
Received:
19
May
2006
Revised:
5
September
2006
Let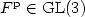 
be the plastic deformation from the multiplicative decomposition in elasto-plasticity. We show that the geometric dislocation density tensor of Gurtin in the form ![${\rm Curl}[{F^{\rm p}}]\cdot (F^{\rm p})^T$](/articles/cocv/abs/2008/01/cocv0632/cocv0632_tex_eq2.png)
applied to rotations controls the gradient in the sense that pointwise
![$ \forall R \in C^1(\mathbb{R}^3, {\rm SO}(3)): \Arrowvert {\rm Curl}[R] \cdot R^T \Arrowvert_{\mathbb{M}^{3\times3}}^2 \ge \frac{1}{2} \Arrowvert{\rm D}R\Arrowvert_{\mathbb{R}^{27}}^2$](/articles/cocv/abs/2008/01/cocv0632/cocv0632_tex_eq3.png)
.
This result complements rigidity results
[Friesecke, James and Müller, Comme Pure Appl. Math. 55 (2002) 1461–1506; John, Comme Pure Appl. Math. 14 (1961) 391–413; Reshetnyak, Siberian Math. J. 8 (1967) 631–653)] as well as an associated linearized theorem saying that
![$ \forall A \in C^1(\mathbb{R}^3, \mathfrak{so}(3)): \Arrowvert {\rm Curl}[A]\Arrowvert_{\mathbb{M}^{3\times3}}^2 \ge \frac{1}{2} \Arrowvert{\rm D}A\Arrowvert_{\mathbb{R}^{27}}^2 = \Arrowvert\nabla{\rm axl}[A]\Arrowvert_{\mathbb{R}^9}^2$](/articles/cocv/abs/2008/01/cocv0632/cocv0632_tex_eq4.png)
.
Mathematics Subject Classification: 74A35 / 74E15 / 74G65 / 74N15 / 53AXX / 53B05
Key words: Rotations / polar-materials / microstructure / dislocation density / rigidity / differential geometry / structured continua
© EDP Sciences, SMAI, 2007
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.