| Issue |
ESAIM: COCV
Volume 14, Number 1, January-March 2008
|
|
|---|---|---|
| Page(s) | 105 - 147 | |
| DOI | https://doi.org/10.1051/cocv:2007047 | |
| Published online | 21 September 2007 | |
Controllablity of a quantum particle in a 1D variable domain
CMLA, ENS Cachan, 61 avenue du président Wilson, 94235 Cachan cedex, France; Karine.Beauchard@cmla.ens-cachan.fr
Received:
2
January
2006
Revised:
10
July
2006
We consider a quantum particle in a 1D infinite square potential well with variable length. It is a nonlinear control system in which the state is the wave function ϕ of the particle and the control is the length l(t) of the potential well. We prove the following controllability result :
given 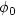 close enough to an eigenstate corresponding to the length l = 1 and
close enough to an eigenstate corresponding to the length l = 1 and 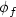 close enough to another eigenstate corresponding to the length l=1, there exists a continuous function
close enough to another eigenstate corresponding to the length l=1, there exists a continuous function ![$l:[0,T] \rightarrow \mathbb{R}^{*}_{+}$](/articles/cocv/abs/2008/01/cocv0601/cocv0601_tex_eq3.png) with T > 0, such that l(0) = 1 and l(T) = 1, and which moves the wave function from
with T > 0, such that l(0) = 1 and l(T) = 1, and which moves the wave function from 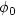 to
to 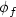 in time T.
In particular, we can move the wave function from one eigenstate to another one by acting on the length of the potential well in a suitable way.
Our proof relies on local controllability results proved with moment theory,
a Nash-Moser implicit function theorem and expansions to the second order.
in time T.
In particular, we can move the wave function from one eigenstate to another one by acting on the length of the potential well in a suitable way.
Our proof relies on local controllability results proved with moment theory,
a Nash-Moser implicit function theorem and expansions to the second order.
Mathematics Subject Classification: 35B37 / 35Q55 / 93B05 / 93C20
Key words: Controllability / Schrödinger equation / Nash-Moser theorem / moment theory
© EDP Sciences, SMAI, 2007
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


