| Issue |
ESAIM: COCV
Volume 16, Number 2, April-June 2010
|
|
|---|---|---|
| Page(s) | 275 - 297 | |
| DOI | https://doi.org/10.1051/cocv:2008075 | |
| Published online | 19 December 2008 | |
Projective Reeds-Shepp car on S2 with quadratic cost
1
LE2i, CNRS UMR5158, Université de Bourgogne, 9 avenue Alain Savary - BP 47870,
21078 Dijon Cedex, France.
2
SISSA, via Beirut 2-4, 34014 Trieste, Italy. boscain@sissa.it; rossifr@sissa.it
Received:
30
May
2008
Fix two points 
and two directions (without orientation) 
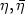of the velocities in these points. In this paper we are interested to the problem of minimizing the cost
![$J[\gamma]=\int_0^T \left({\g}_{\gamma(t)}(\dot\gamma(t),\dot\gamma(t))+ K^2_{\gamma(t)}{\g}_{\gamma(t)}(\dot\gamma(t),\dot\gamma(t)) \right) ~{\rm d}t$](/articles/cocv/abs/2010/02/cocv0846/cocv0846_tex_eq3.png)
along all smooth curves starting from x with direction η and ending in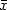 
with direction 
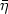. Here g is the standard Riemannian metric on S2 and 
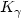is the corresponding geodesic curvature.
The interest of this problem comes from mechanics and geometry of vision. It can be formulated as a sub-Riemannian problem on the lens space L(4,1).
We compute the global solution for this problem: an interesting feature is that some optimal geodesics present cusps. The cut locus is a stratification with non trivial topology.
Mathematics Subject Classification: 49J15 / 53C17
Key words: Carnot-Caratheodory distance / geometry of vision / lens spaces / global cut locus
© EDP Sciences, SMAI, 2008
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.