| Issue |
ESAIM: COCV
Volume 12, Number 3, July 2006
|
|
|---|---|---|
| Page(s) | 564 - 614 | |
| DOI | https://doi.org/10.1051/cocv:2006013 | |
| Published online | 20 June 2006 | |
Gradient flows of non convex functionals in Hilbert spaces and applications
Dipartimento di Matematica “F. Casorati”, Università di Pavia. Via
Ferrata, 1 – 27100 Pavia, Italy;
riccarda.rossi@unipv.it; giuseppe.savare@unipv.it
Received:
3
May
2005
This paper addresses the Cauchy problem for the
gradient flow equation in a Hilbert space 
![\[ \begin{cases} u'(t)+ \partial_{\ell}\phi(u(t))\ni f(t) &\text{{\it a.e.}\ in }(0,T), u(0)=u_0, \end{cases} \]](/articles/cocv/abs/2006/03/cocv0535/cocv0535_tex_eq2.png) where
where ![$\phi: \mathcal{H} \to (-\infty,+\infty]$](/articles/cocv/abs/2006/03/cocv0535/cocv0535_tex_eq3.png) is a proper,
lower semicontinuous functional which is not supposed to be a
(smooth perturbation of a) convex functional and
is a proper,
lower semicontinuous functional which is not supposed to be a
(smooth perturbation of a) convex functional and 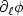 is
(a suitable limiting version of) its subdifferential.
We will present some new existence results for the solutions of the
equation by exploiting a variational approximation
technique, featuring some ideas from the theory of Minimizing Movements
and of Young measures.
Our analysis
is also motivated by some models describing phase transitions
phenomena, leading to
systems of evolutionary PDEs which have a common
underlying gradient flow structure:
in particular, we will focus on
quasistationary models, which exhibit
highly non convex Lyapunov functionals.
is
(a suitable limiting version of) its subdifferential.
We will present some new existence results for the solutions of the
equation by exploiting a variational approximation
technique, featuring some ideas from the theory of Minimizing Movements
and of Young measures.
Our analysis
is also motivated by some models describing phase transitions
phenomena, leading to
systems of evolutionary PDEs which have a common
underlying gradient flow structure:
in particular, we will focus on
quasistationary models, which exhibit
highly non convex Lyapunov functionals.
Mathematics Subject Classification: 35A15 / 35K50 / 35K85 / 58D25 / 80A22
Key words: Evolution problems / gradient flows / minimizing movements / Young measures / phase transitions / quasistationary models.
© EDP Sciences, SMAI, 2006
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


