| Issue |
ESAIM: COCV
Volume 13, Number 1, January-March 2007
|
|
|---|---|---|
| Page(s) | 93 - 106 | |
| DOI | https://doi.org/10.1051/cocv:2006017 | |
| Published online | 14 February 2007 | |
Existence of optimal maps in the reflector-type problems
1
School of Mathematics, Georgia
Institute of Technology,
Atlanta, GA 30332, USA; gangbo@math.gatech.edu
2
Dept. of Mathematics and Computer Science,
Emory University, Atlanta, GA 30322, USA;
oliker@mathcs.emory.edu
Received:
4
May
2005
Revised:
9
September
2005
In this paper, we
consider probability measures μ and ν on a d-dimensional
sphere in  and cost functions of the form
and cost functions of the form
 that generalize those arising in geometric optics where
that generalize those arising in geometric optics where  We prove that if μ and ν vanish on
We prove that if μ and ν vanish on  -rectifiable sets,
if |l'(t)|>0,
-rectifiable sets,
if |l'(t)|>0,  and
and 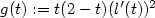 is monotone then there
exists a unique optimal map To that transports μ onto
is monotone then there
exists a unique optimal map To that transports μ onto  where
optimality is measured against c. Furthermore,
where
optimality is measured against c. Furthermore, 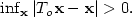 Our approach is based on direct variational arguments.
In the special case when
Our approach is based on direct variational arguments.
In the special case when
 existence of optimal maps on the
sphere was obtained earlier in [Glimm and Oliker, J. Math. Sci. 117 (2003) 4096-4108]
and [Wang, Calculus of Variations and PDE's 20 (2004) 329-341] under more restrictive assumptions. In these studies, it was assumed that
either μ and ν are absolutely
continuous with respect to the d-dimensional Haussdorff measure, or they
have disjoint supports.
Another aspect of interest
in this work is that it is in contrast with the work in
[Gangbo and McCann, Quart. Appl. Math. 58 (2000) 705-737] where it is proved that when l(t)=t then
existence of an optimal map fails when μ and ν are
supported by Jordan surfaces.
existence of optimal maps on the
sphere was obtained earlier in [Glimm and Oliker, J. Math. Sci. 117 (2003) 4096-4108]
and [Wang, Calculus of Variations and PDE's 20 (2004) 329-341] under more restrictive assumptions. In these studies, it was assumed that
either μ and ν are absolutely
continuous with respect to the d-dimensional Haussdorff measure, or they
have disjoint supports.
Another aspect of interest
in this work is that it is in contrast with the work in
[Gangbo and McCann, Quart. Appl. Math. 58 (2000) 705-737] where it is proved that when l(t)=t then
existence of an optimal map fails when μ and ν are
supported by Jordan surfaces.
Mathematics Subject Classification: 49 / 35J65
Key words: Mass transport / reflector problem / Monge-Ampere equation.
© EDP Sciences, SMAI, 2007
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


