| Issue |
ESAIM: COCV
Volume 15, Number 2, April-June 2009
|
|
|---|---|---|
| Page(s) | 279 - 294 | |
| DOI | https://doi.org/10.1051/cocv:2008024 | |
| Published online | 28 March 2008 | |
Unique continuation property near a corner and its fluid-structure controllability consequences
1
Departamento de
Ingenería Matemática and Centro
de Modelamiento Matemático (UMI 2807 CNRS), FCFM Universidad de Chile,
Casilla 170/3 - Correo 3, Santiago, Chile; axosses@dim.uchile.cl
2
Laboratoire de Mathématiques de Versailles, UMR 8100,
Université de Versailles St-Quentin, 45 avenue des États-Unis, 78035
Versailles cedex, France; Jean-Pierre.Puel@math.uvsq.fr
Received:
19
September
2005
Revised:
27
January
2006
Revised:
27
September
2007
We study a non standard unique continuation property for the
biharmonic spectral problem  in a 2D
corner with homogeneous Dirichlet boundary conditions and a
supplementary third order boundary condition on one side of the
corner. We prove that if the corner has an angle
in a 2D
corner with homogeneous Dirichlet boundary conditions and a
supplementary third order boundary condition on one side of the
corner. We prove that if the corner has an angle 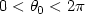 ,
,
 and
and 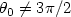 , a unique continuation
property holds. Approximate controllability of a 2-D linear
fluid-structure problem follows from this property, with a control
acting on the elastic side of a corner in a domain containing a
Stokes fluid. The proof of
the main result is based in a power series expansion of the
eigenfunctions near the corner, the resolution of a coupled infinite
set of finite dimensional linear systems, and a result of
Kozlov, Kondratiev and Mazya, concerning the absence of
strong zeros for the biharmonic operator [Math. USSR Izvestiya
34 (1990) 337–353]. We also show how the same methodology
used here can be adapted to exclude domains with corners to have a local
version of the Schiffer property for the Laplace operator.
, a unique continuation
property holds. Approximate controllability of a 2-D linear
fluid-structure problem follows from this property, with a control
acting on the elastic side of a corner in a domain containing a
Stokes fluid. The proof of
the main result is based in a power series expansion of the
eigenfunctions near the corner, the resolution of a coupled infinite
set of finite dimensional linear systems, and a result of
Kozlov, Kondratiev and Mazya, concerning the absence of
strong zeros for the biharmonic operator [Math. USSR Izvestiya
34 (1990) 337–353]. We also show how the same methodology
used here can be adapted to exclude domains with corners to have a local
version of the Schiffer property for the Laplace operator.
Mathematics Subject Classification: 35B60 / 35B37
Key words: Continuation of solutions of PDE / fluid-structure control / domains with corners
© EDP Sciences, SMAI, 2008
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


