Oscillations and concentrations generated by -free mappings and weak lower semicontinuity of integral functionals

Irene Fonseca; Martin Kružík

doi:10.1051/cocv/2009006

All issues

Volume 16 / No 2 (April-June 2010)

ESAIM: COCV, 16 2 (2010) 472-502

Abstract

Free Access

Issue		ESAIM: COCV Volume 16, Number 2, April-June 2010


Page(s)		472 - 502
DOI		https://doi.org/10.1051/cocv/2009006
Published online		21 April 2009

ESAIM: COCV 16 (2010) 472-502

Oscillations and concentrations generated by ${\mathcal A}$ -free mappings and weak lower semicontinuity of integral functionals

Irene Fonseca¹ and Martin Kružík²^,3

¹ Department of Mathematical Sciences, Carnegie Mellon University, Pittsburgh, PA 15213, USA. fonseca@andrew.cmu.edu
² Institute of Information Theory and Automation of the ASCR, Pod vodárenskou věží 4, 182 08 Praha 8, Czech Republic.
³ Faculty of Civil Engineering, Czech Technical University, Thákurova 7, 166 29 Praha 6, Czech Republic. kruzik@utia.cas.cz

Received: 3 October 2008
Revised: 9 December 2008

Abstract

DiPerna's and Majda's generalization of Young measures is used to describe oscillations and concentrations in sequences of maps 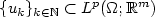$\{u_k\}_{k\in{\mathbb N}} \subset L^p(\Omega;{\mathbb R}^m)$ satisfying a linear differential constraint 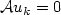${\mathcal A}u_k=0$ . Applications to sequential weak lower semicontinuity of integral functionals on ${\mathcal A}$ -free sequences and to weak continuity of determinants are given. 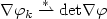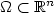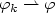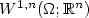In particular, we state necessary and sufficient conditions for weak* convergence of det $\nabla\varphi_k\stackrel{*}{\rightharpoonup}{\rm det}\nabla\varphi$ in measures on the closure of $\Omega\subset{\mathbb R}^n$ if $\varphi_k\rightharpoonup\varphi$ in $W^{1,n}(\Omega;{\mathbb R}^n)$ . This convergence holds, for example, under Dirichlet boundary conditions. 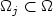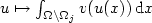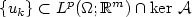Further, we formulate a Biting-like lemma precisely stating which subsets $\Omega_j\subset \Omega$ must be removed to obtain weak lower semicontinuity of $u\mapsto\int_{\Omega\setminus\Omega_j} v(u(x))\,{\rm d}x$ along $\{u_k\}\subset L^p(\Omega;{\mathbb R}^m)\cap{\rm ker}\ {\mathcal A}$ . Specifically, 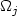$\Omega_j$ are arbitrarily thin “boundary layers”.

Mathematics Subject Classification: 49J45 / 35B05

Key words: Concentrations / oscillations / Young measures

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.