| Issue |
ESAIM: COCV
Volume 20, Number 3, July-September 2014
|
|
|---|---|---|
| Page(s) | 748 - 770 | |
| DOI | https://doi.org/10.1051/cocv/2013082 | |
| Published online | 27 May 2014 | |
Curve cuspless reconstruction via sub-Riemannian geometry∗,∗∗
1
Centre National de Recherche Scientifique (CNRS), CMAP, Ecole
Polytechnique, Route de Saclay, 91128
Palaiseau Cedex,
France, and Team GECO, INRIA-Centre de Recherche
Saclay
ugo.boscain@polytecnique.edu
2
Eindhoven University of Technology, P.O. Box 513, 5600 MB, Eindhoven, The Netherlands.
Department of Mathematics and Computer Science
R.Duits@tue.nl
3
Aix-Marseille Univ, LSIS, 13013, Marseille, France
francesco.rossi@lsis.org
4 Program Systems Institute
Pereslavl-Zalessky, Russia
sachkov@sys.botik.ru
Received: 31 July 2013
We consider the problem of minimizing
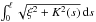for a planar curve having fixed
initial and final positions and directions. The total length ℓ is free. Here
s is the
arclength parameter, K(s) is the curvature of the curve
and ξ > 0 is a fixed constant. This problem comes from a model of geometry of
vision due to Petitot, Citti and Sarti. We study existence of local and global minimizers
for this problem. We prove that if for a certain choice of boundary conditions there is no
global minimizer, then there is neither a local minimizer nor a geodesic. We finally give
properties of the set of boundary conditions for which there exists a solution to the
problem.
Mathematics Subject Classification: 94A08 / 49J15
Key words: Curve reconstruction / generalized pontryagin maximum principle
The authors wish to thank Arpan Ghosh and Tom Dela Haije, Eindhoven University of Technology, for the contribution with numerical computations and figures.
This research has been supported by the European Research Council, ERC StG 2009 “GeCoMethods”, contract number 239748, by the ANR “GCM”, program “Blanc–CSD” project number NT09-504490, by the DIGITEO project “CONGEO”, by Russian Foundation for Basic Research, Project No. 12-01-00913-a, and by the Ministry of Education and Science of Russia within the federal program “Scientific and Scientific-Pedagogical Personnel of Innovative Russia”, contract No. 8209.
© EDP Sciences, SMAI, 2014
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.