| Issue |
ESAIM: COCV
Volume 23, Number 3, July-September 2017
|
|
|---|---|---|
| Page(s) | 1145 - 1177 | |
| DOI | https://doi.org/10.1051/cocv/2016028 | |
| Published online | 12 May 2017 | |
Bifurcation and segregation in quadratic two-populations mean field games systems
1 Dipartimento di Matematica, Università di Milano, via Cesare Saldini 50, 20133 Milano, Italy
marco.cirant@unimi.it
2 Dipartimento di Matematica, Politecnico di Milano, piazza Leonardo da Vinci 32, 20133 Milano, Italy
gianmaria.verzini@polimi.it
Received: 14 January 2016
Revised: 11 May 2016
Accepted: 21 May 2016
We search for non-constant normalized solutions to the semilinear elliptic system 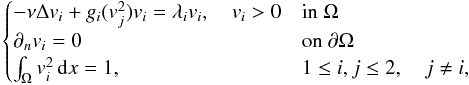 where ν > 0, Ω ⊂ RN is smooth and bounded, the functions gi are positive and increasing, and both the functions vi and the parameters λi are unknown. This system is obtained, via the Hopf−Cole transformation, from a two-populations ergodic Mean Field Games system, which describes Nash equilibria in differential games with identical players. In these models, each population consists of a very large number of indistinguishable rational agents, aiming at minimizing some long-time average criterion. Firstly, we discuss existence of nontrivial solutions, using variational methods when gi(s) = s, and bifurcation ones in the general case; secondly, for selected families of nontrivial solutions, we address the appearing of segregation in the vanishing viscosity limit, i.e.
where ν > 0, Ω ⊂ RN is smooth and bounded, the functions gi are positive and increasing, and both the functions vi and the parameters λi are unknown. This system is obtained, via the Hopf−Cole transformation, from a two-populations ergodic Mean Field Games system, which describes Nash equilibria in differential games with identical players. In these models, each population consists of a very large number of indistinguishable rational agents, aiming at minimizing some long-time average criterion. Firstly, we discuss existence of nontrivial solutions, using variational methods when gi(s) = s, and bifurcation ones in the general case; secondly, for selected families of nontrivial solutions, we address the appearing of segregation in the vanishing viscosity limit, i.e. 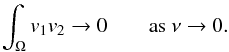
Mathematics Subject Classification: 35J47 / 49N70 / 35B25 / 35B32
Key words: Singularly perturbed problems / normalized solutions to semilinear elliptic systems / multi-population differential games
© EDP Sciences, SMAI 2017
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


