| Issue |
ESAIM: COCV
Volume 6, 2001
|
|
|---|---|---|
| Page(s) | 291 - 331 | |
| DOI | https://doi.org/10.1051/cocv:2001112 | |
| Published online | 15 August 2002 | |
On the Lp-stabilization of the double integrator subject to input saturation
Université Paris XI,
Département de Mathématiques, 91405 Orsay, France;
Yacine.Chitour@math.u-psud.fr.
Received:
22
November
1999
Received:
January
2001
We consider a finite-dimensional control system  , such that there exists a feedback stabilizer k
that renders
, such that there exists a feedback stabilizer k
that renders  globally asymptotically
stable. Moreover, for (H,p,q) with H an output map and
globally asymptotically
stable. Moreover, for (H,p,q) with H an output map and 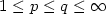 , we assume that there exists a
, we assume that there exists a  -function
α such that
-function
α such that  , where xu is the
maximal solution of
, where xu is the
maximal solution of  ,
corresponding to u and to the initial condition x(0)=0. Then, the
gain function
,
corresponding to u and to the initial condition x(0)=0. Then, the
gain function  of (H,p,q) given by 14.5cm
of (H,p,q) given by 14.5cm
 is well-defined. We call profile of k for (H,p,q) any
is well-defined. We call profile of k for (H,p,q) any
 -function which is of the same order of magnitude
as
-function which is of the same order of magnitude
as  . For the double integrator subject to input saturation
and stabilized by
. For the double integrator subject to input saturation
and stabilized by
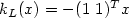 , we determine the profiles corresponding to the main
output maps. In particular, if
, we determine the profiles corresponding to the main
output maps. In particular, if  is used to denote the standard
saturation function, we show that the L2-gain from the output of the
saturation nonlinearity to u of the system
is used to denote the standard
saturation function, we show that the L2-gain from the output of the
saturation nonlinearity to u of the system  with
with  , is finite. We also provide a class of feedback
stabilizers kF that have a linear profile for (x,p,p),
, is finite. We also provide a class of feedback
stabilizers kF that have a linear profile for (x,p,p),  .
For instance,
we show that the L2-gains from x and
.
For instance,
we show that the L2-gains from x and  to u of the
system
to u of the
system  with
with  ,
are finite.
,
are finite.
Mathematics Subject Classification: 93D15 / 93D21 / 93D30
Key words: Nonlinear control systems / Lp-stabilization / input-to-state stability / finite-gain stability / input saturation / Lyapunov function.
© EDP Sciences, SMAI, 2001
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


