| Issue |
ESAIM: COCV
Volume 7, 2002
|
|
|---|---|---|
| Page(s) | 443 - 470 | |
| DOI | https://doi.org/10.1051/cocv:2002063 | |
| Published online | 15 September 2002 | |
Equi-integrability results for 3D-2D dimension reduction problems
Department of Mathematical Sciences,
Carnegie Mellon University, Pittsburgh, PA 15213, USA; mbocea@andrew.cmu.edu.
Received:
7
February
2002
3D-2D asymptotic analysis for thin structures rests on the mastery
of scaled gradients 
bounded in 
Here it is shown that, up to a
subsequence, 
may be decomposed as 
where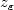 
carries all the concentration effects, i.e.
is
equi-integrable, and 
captures the oscillatory behavior,
i.e.
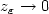in measure. In addition, if 
is
a recovering sequence then 
nearby
Mathematics Subject Classification: 49J45 / 74B20 / 74G10 / 74K15 / 74K35
Key words: Equi-integrability / dimension reduction / lower semicontinuity / maximal function / oscillations / concentrations / quasiconvexity.
© EDP Sciences, SMAI, 2002
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.