| Issue |
ESAIM: COCV
Volume 7, 2002
|
|
|---|---|---|
| Page(s) | 471 - 493 | |
| DOI | https://doi.org/10.1051/cocv:2002064 | |
| Published online | 15 September 2002 | |
Tracking with prescribed transient behaviour
1
Institute of Mathematics, Technical
University Ilmenau, Weimarer Straße 25, 98693 Ilmenau,
Germany; ilchmann@mathematik.tu-ilmenau.de.
2
Department of Mathematical Sciences,
University of Bath, Claverton Down, Bath BA2 7AY, UK; epr@maths.bath.ac.uk.
3
School of Mathematics and Statistics, University of
Birmingham, Edgbaston, Birmingham B15 2TT, UK; C.J.Sangwin@bham.ac.uk.
Received:
7
February
2002
Revised:
17
April
2002
Universal tracking control is investigated in the context of a
class S of M-input, M-output dynamical systems modelled by
functional differential equations. The class
encompasses a wide variety of nonlinear and infinite-dimensional
systems and contains – as a prototype subclass – all
finite-dimensional linear single-input single-output minimum-phase
systems with positive high-frequency gain. The control objective
is to ensure that, for an arbitrary  -valued reference signal
r of class W1,∞ (absolutely continuous and bounded
with essentially bounded derivative) and every system of class S, the tracking error e between plant output and reference
signal evolves within a prespecified performance envelope or
funnel in the sense that
-valued reference signal
r of class W1,∞ (absolutely continuous and bounded
with essentially bounded derivative) and every system of class S, the tracking error e between plant output and reference
signal evolves within a prespecified performance envelope or
funnel in the sense that  for all t ≥ 0, where φ a prescribed real-valued function of class
W1,∞ with the property that φ(s) > 0 for all s >
0 and
for all t ≥ 0, where φ a prescribed real-valued function of class
W1,∞ with the property that φ(s) > 0 for all s >
0 and  . A simple (neither
adaptive nor dynamic) error feedback control of the form
. A simple (neither
adaptive nor dynamic) error feedback control of the form  is introduced which achieves the
objective whilst maintaining boundedness of the control and of the
scalar gain
is introduced which achieves the
objective whilst maintaining boundedness of the control and of the
scalar gain
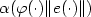 .
.
Mathematics Subject Classification: 93D15 / 93C30 / 34K20
Key words: Nonlinear systems / functional differential equations / feedback control / tracking / transient behaviour.
© EDP Sciences, SMAI, 2002
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


