| Issue |
ESAIM: COCV
Volume 8, 2002
A tribute to JL Lions
|
|
|---|---|---|
| Page(s) | 603 - 619 | |
| DOI | https://doi.org/10.1051/cocv:2002036 | |
| Published online | 15 August 2002 | |
On a variant of Korn's inequality arising in statistical mechanics
1
Centre de Mathématiques et Leurs Applications,
École Normale Supérieure de Cachan,
61 avenue du Président Wilson,
94235 Cachan, France;
desville@cmla.ens-cachan.fr.
2
UMPA, École Normale Supérieure de Lyon,
69364 Lyon Cedex 07, France; cvillani@umpa.ens-lyon.fr.
Received:
4
February
2002
We state and prove a Korn-like inequality for a vector field in a
bounded open set of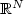 
, satisfying a tangency boundary condition.
This inequality, which is crucial in our study of the trend towards
equilibrium for dilute gases, holds true if and only if the domain is not
axisymmetric. We give quantitative, explicit estimates on how the
departure from axisymmetry affects the constants; a Monge–Kantorovich
minimization problem naturally arises in this process.
Variants in the axisymmetric case are briefly discussed.
Mathematics Subject Classification: 49J40 / 82C40 / 76P05
Key words: Korn's inequality / Boltzmann equation / Monge–Kantorovich mass transportation problem.
© EDP Sciences, SMAI, 2002
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.