| Issue |
ESAIM: COCV
Volume 10, Number 1, January 2004
|
|
|---|---|---|
| Page(s) | 142 - 167 | |
| DOI | https://doi.org/10.1051/cocv:2003040 | |
| Published online | 15 February 2004 | |
Newton and conjugate gradient for harmonic maps from the disc into the sphere
Centre de Mathématiques et de Leurs Applications,
École Normale Supérieure de Cachan,
61 avenue du Président Wilson,
94235 Cachan Cedex, France; Morgan.Pierre@cmla.ens-cachan.fr.
Received:
28
January
2003
We compute numerically the minimizers of the Dirichlet energy
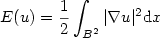 among maps
among maps 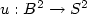 from the unit disc into the unit sphere that satisfy a boundary condition and a degree condition.
We use a Sobolev gradient algorithm for the minimization and we prove that its continuous version preserves the degree. For the discretization of the problem we use continuous P1 finite elements. We propose an original mesh-refining strategy needed to preserve the degree with the discrete version of the algorithm (which is a preconditioned projected gradient). In order to improve the convergence, we generalize to manifolds the classical Newton and conjugate gradient algorithms. We give a proof of the quadratic convergence of the Newton algorithm for manifolds in a general setting.
from the unit disc into the unit sphere that satisfy a boundary condition and a degree condition.
We use a Sobolev gradient algorithm for the minimization and we prove that its continuous version preserves the degree. For the discretization of the problem we use continuous P1 finite elements. We propose an original mesh-refining strategy needed to preserve the degree with the discrete version of the algorithm (which is a preconditioned projected gradient). In order to improve the convergence, we generalize to manifolds the classical Newton and conjugate gradient algorithms. We give a proof of the quadratic convergence of the Newton algorithm for manifolds in a general setting.
Mathematics Subject Classification: 58E20 / 78M10 / 65N30 / 90C53
Key words: Harmonic maps / finite elements / mesh-refinement / Sobolev gradient / Newton algorithm / conjugate gradient.
© EDP Sciences, SMAI, 2004
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


