| Issue |
ESAIM: COCV
Volume 10, Number 2, April 2004
|
|
|---|---|---|
| Page(s) | 243 - 258 | |
| DOI | https://doi.org/10.1051/cocv:2004005 | |
| Published online | 15 March 2004 | |
The steepest descent dynamical system with control. Applications to constrained minimization
Laboratoire LACO, Faculté des Sciences, 123 avenue Albert Thomas,
87060 Limoges Cedex, France; alexandre.cabot@unilim.fr.
Received:
17
February
2003
Let H be a real Hilbert space,  a
convex function of class
a
convex function of class  that we wish to minimize under the convex
constraint S.
A classical approach consists in following the trajectories of the generalized
steepest descent system (cf. Brézis [CITE]) applied
to the non-smooth function
that we wish to minimize under the convex
constraint S.
A classical approach consists in following the trajectories of the generalized
steepest descent system (cf. Brézis [CITE]) applied
to the non-smooth function  . Following Antipin [1], it is also possible to use a
continuous gradient-projection system.
We propose here an alternative method as follows:
given a smooth convex function
. Following Antipin [1], it is also possible to use a
continuous gradient-projection system.
We propose here an alternative method as follows:
given a smooth convex function  whose critical points coincide
with S
and a control parameter
whose critical points coincide
with S
and a control parameter  tending to zero,
we consider the “Steepest Descent and Control” system
tending to zero,
we consider the “Steepest Descent and Control” system
![\[(SDC) \qquad \dot{x}(t)+\nabla \Phi_0(x(t))+\varepsilon(t)\, \nabla \Phi_1(x(t))=0,\]](/articles/cocv/abs/2004/02/cocv0311/cocv0311_tex_eq6.png) where
the control ε satisfies
where
the control ε satisfies  . This last condition ensures that ε “slowly” tends
to 0. When H is finite dimensional, we then prove that
. This last condition ensures that ε “slowly” tends
to 0. When H is finite dimensional, we then prove that
 and we give sufficient conditions under which
and we give sufficient conditions under which 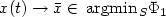 .
We end the paper by numerical experiments allowing to compare
the (SDC) system with the other systems already mentioned.
.
We end the paper by numerical experiments allowing to compare
the (SDC) system with the other systems already mentioned.
Mathematics Subject Classification: 34A12 / 34D05 / 34G20 / 34H05 / 37N40
Key words: Dissipative dynamical system / steepest descent method / constrained optimization / convex minimization / asymptotic behaviour / non-linear oscillator.
© EDP Sciences, SMAI, 2004
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


