Asymptotic behavior of second-order dissipative evolution equations combining potential with non-potential effects^*

¹ Institut de Mathématiques et de Modélisation de Montpellier, UMR CNRS 5149, CC 51, Université Montpellier II, place Eugène Bataillon, 34095 Montpellier Cedex 5, France. attouch@math.univ-montp2.fr.
² Université des Antilles-Guyane, D.S.I., CEREGMIA, Campus de Schoelcher, 97233 Schoelcher Cedex, Martinique, France. Paul-Emile.Mainge@martinique.univ-ag.fr

Received: 1 May 2009
Revised: 18 December 2009
Revised: 9 April 2010

Abstract

In the setting of a real Hilbert space , we investigate the asymptotic behavior, as time t goes to infinity, of trajectories of second-order evolution equations

           ü(t) + γ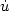(t) + ∇ϕ(u(t)) + A(u(t)) = 0,

where ∇ϕ is the gradient operator of a convex differentiable potential function ϕ : , A : is a maximal monotone operator which is assumed to be λ-cocoercive, and γ > 0 is a damping parameter. Potential and non-potential effects are associated respectively to ∇ϕ and A. Under condition λγ² > 1, it is proved that each trajectory asymptotically weakly converges to a zero of ∇ϕ + A. This condition, which only involves the non-potential operator and the damping parameter, is sharp and consistent with time rescaling. Passing from weak to strong convergence of the trajectories is obtained by introducing an asymptotically vanishing Tikhonov-like regularizing term. As special cases, we recover the asymptotic analysis of the heavy ball with friction dynamic attached to a convex potential, the second-order gradient-projection dynamic, and the second-order dynamic governed by the Yosida approximation of a general maximal monotone operator. The breadth and flexibility of the proposed framework is illustrated through applications in the areas of constrained optimization, dynamical approach to Nash equilibria for noncooperative games, and asymptotic stabilization in the case of a continuum of equilibria.