| Issue |
ESAIM: COCV
Volume 12, Number 1, January 2006
|
|
|---|---|---|
| Page(s) | 64 - 92 | |
| DOI | https://doi.org/10.1051/cocv:2005034 | |
| Published online | 15 December 2005 | |
New convexity conditions in the calculus of variations and compensated compactness theory
1
Cardinal Stefan Wyszyński University,
ul. Dewajtis 5, 01-815 Warszawa, Poland;
chelminski@uksw.edu.pl
2
University of Constance,
Universitätsstr. 10, 78464 Konstanz, Germany
3
Institute of Mathematics,
Warsaw University, ul. Banacha 2,
02–097 Warszawa, Poland; kalamajs@mimuw.edu.pl
Received:
22
March
2004
Revised:
10
August
2004
We consider the lower semicontinuous functional of the form
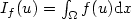 where u satisfies a given
conservation law defined by differential operator of degree one
with constant coefficients. We show that under certain constraints
the well known Murat and Tartar's Λ-convexity condition
for the integrand f extends to the new geometric conditions
satisfied on four dimensional symplexes. Similar conditions on
three dimensional symplexes were recently obtained by the second
author. New conditions apply to quasiconvex functions.
where u satisfies a given
conservation law defined by differential operator of degree one
with constant coefficients. We show that under certain constraints
the well known Murat and Tartar's Λ-convexity condition
for the integrand f extends to the new geometric conditions
satisfied on four dimensional symplexes. Similar conditions on
three dimensional symplexes were recently obtained by the second
author. New conditions apply to quasiconvex functions.
Mathematics Subject Classification: 49J10 / 49J45
Key words: Quasiconvexity / rank-one convexity / semicontinuity.
© EDP Sciences, SMAI, 2006
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


