| Issue |
ESAIM: COCV
Volume 12, Number 4, October 2006
|
|
|---|---|---|
| Page(s) | 770 - 785 | |
| DOI | https://doi.org/10.1051/cocv:2006021 | |
| Published online | 11 October 2006 | |
Stabilization of wave systems with input delay in the boundary control
1
Mathematics Department of Tianjin University, Tianjin, 300072, P.R. China; gqxu@tju.edu.cn
2
Mathematics Department of Hong Kong University, Hong Kong, P.R. China; spyung@hku.hk
3
Applied Mathematics Department of the Hong Kong Polytechnic University, Hong Kong, P.R. China; malblkli@polyu.edu.hk
Received:
1
July
2004
Revised:
10
May
2005
Revised:
13
October
2005
In the present paper, we consider a wave system that is fixed at one end and a boundary control input possessing a partial time delay of weight 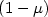 is applied over the other end. Using a simple boundary velocity feedback law, we show that the closed loop system
generates a C0 group of linear operators. After a spectral analysis, we show
that the closed loop system is a Riesz one, that is, there is a sequence of eigenvectors and
generalized eigenvectors that forms a Riesz basis for the state Hilbert space.
Furthermore, we show that when the weight
is applied over the other end. Using a simple boundary velocity feedback law, we show that the closed loop system
generates a C0 group of linear operators. After a spectral analysis, we show
that the closed loop system is a Riesz one, that is, there is a sequence of eigenvectors and
generalized eigenvectors that forms a Riesz basis for the state Hilbert space.
Furthermore, we show that when the weight  , for any time delay,
we can choose a suitable feedback gain so that the closed loop system is exponentially stable. When
, for any time delay,
we can choose a suitable feedback gain so that the closed loop system is exponentially stable. When  , we show that the system is at most asymptotically stable. When
, we show that the system is at most asymptotically stable. When  , the system is always unstable.
, the system is always unstable.
Mathematics Subject Classification: 34H05 / 49J25 / 49K25 / 93D15
Key words: Wave equation / time delay / stabilization / Riesz basis.
© EDP Sciences, SMAI, 2006
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


