| Issue |
ESAIM: COCV
Volume 12, Number 4, October 2006
|
|
|---|---|---|
| Page(s) | 795 - 815 | |
| DOI | https://doi.org/10.1051/cocv:2006023 | |
| Published online | 11 October 2006 | |
Graph selectors and viscosity solutions on Lagrangian manifolds
University of Sheffield, Dept. of Automatic Control and Systems Engineering,
Mappin Street, Sheffield, S1 3JD, UK; david@mccaffrey275.fsnet.co.uk
Received:
24
August
2005
Let  be a Lagrangian submanifold of
be a Lagrangian submanifold of 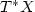 for some closed
manifold X. Let
for some closed
manifold X. Let 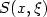 be a generating function for
be a generating function for  which
is quadratic at infinity, and let W(x) be the corresponding graph selector
for
which
is quadratic at infinity, and let W(x) be the corresponding graph selector
for 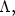 in the sense of Chaperon-Sikorav-Viterbo, so that there
exists a subset
in the sense of Chaperon-Sikorav-Viterbo, so that there
exists a subset  of measure zero such that W is Lipschitz
continuous on X, smooth on
of measure zero such that W is Lipschitz
continuous on X, smooth on 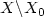 and
and 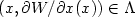 for
for 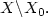 Let H(x,p)=0 for
Let H(x,p)=0 for 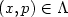 . Then W is a classical solution to
. Then W is a classical solution to 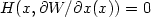 on
on 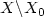 and extends to a Lipschitz function on the
whole of X. Viterbo refers to W as a variational solution. We prove that
W is also a viscosity solution under some simple and natural conditions.
We also prove that these conditions are satisfied in many cases, including
certain commonly occuring cases where H(x,p) is not convex in p.
and extends to a Lipschitz function on the
whole of X. Viterbo refers to W as a variational solution. We prove that
W is also a viscosity solution under some simple and natural conditions.
We also prove that these conditions are satisfied in many cases, including
certain commonly occuring cases where H(x,p) is not convex in p.
Mathematics Subject Classification: 49L25 / 53D12
Key words: Viscosity solution / Lagrangian manifold / graph selector.
© EDP Sciences, SMAI, 2006
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


