| Issue |
ESAIM: COCV
Volume 13, Number 3, July-September 2007
|
|
|---|---|---|
| Page(s) | 553 - 569 | |
| DOI | https://doi.org/10.1051/cocv:2007026 | |
| Published online | 20 June 2007 | |
Numerical study of a new global minimizer for the Mumford-Shah functional in R3
Université Paris Nord - Institut Galillée, LAGA (Laboratoire d'Analyse Géométrie et Applications), Avenue J.B. Clément, 93430 Villetaneuse, France; merlet@math.univ-paris13.fr
Received:
12
September
2005
Revised:
9
January
2006
In [Progress Math. 233 (2005)], David suggested the existence of a new type of global minimizers for the Mumford-Shah functional in 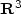 . The singular set of such a new minimizer belongs to a three parameters family of sets
. The singular set of such a new minimizer belongs to a three parameters family of sets  .
We first derive necessary conditions satisfied by global minimizers of this family. Then we are led to study the first eigenvectors of the Laplace-Beltrami operator with Neumann boundary conditions on subdomains of
.
We first derive necessary conditions satisfied by global minimizers of this family. Then we are led to study the first eigenvectors of the Laplace-Beltrami operator with Neumann boundary conditions on subdomains of 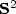 with three reentrant corners. The necessary conditions are constraints on the eigenvalue and on the ratios between the three singular coefficients of the associated eigenvector.
We use numerical methods (Singular Functions Method and Moussaoui's extraction formula) to compute the eigenvalues and the singular coefficients. We conclude that there is no
with three reentrant corners. The necessary conditions are constraints on the eigenvalue and on the ratios between the three singular coefficients of the associated eigenvector.
We use numerical methods (Singular Functions Method and Moussaoui's extraction formula) to compute the eigenvalues and the singular coefficients. We conclude that there is no  for which the necessary conditions are satisfied and this shows that the hypothesis was wrong.
for which the necessary conditions are satisfied and this shows that the hypothesis was wrong.
Mathematics Subject Classification: 35J25 / 49R50 / 65N38
Key words: Mumford-Shah functional / numerical analysis / boundary value problems for second-order / elliptic equations in domains with corners
© EDP Sciences, SMAI, 2007
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


