| Issue |
ESAIM: COCV
Volume 22, Number 2, April-June 2016
|
|
|---|---|---|
| Page(s) | 404 - 416 | |
| DOI | https://doi.org/10.1051/cocv/2015011 | |
| Published online | 08 March 2016 | |
Average-distance problem for parameterized curves
Department of Mathematical Sciences, Carnegie Mellon University, Pittsburgh,
PA, 15213, USA
xinyang@andrew.cmu.edu; slepcev@math.cmu.edu
Received:
15
October
2014
Revised:
8
February
2015
We consider approximating a measure by a parameterized curve subject to length
penalization. That is for a given finite compactly supported measure
μ
, with
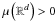 for p ≥ 1 and λ> 0 we consider the
functional
for p ≥ 1 and λ> 0 we consider the
functional
where γ:I → ℝd, I is an interval in ℝ, Γγ = γ(I), and d(x,Γγ) is the distance of x to Γγ. The problem is closely related to the average-distance problem, where the admissible class are the connected sets of finite Hausdorff measure ℋ1, and to (regularized) principal curves studied in statistics. We obtain regularity of minimizers in the form of estimates on the total curvature of the minimizers. We prove that for measures μ supported in two dimensions the minimizing curve is injective if p ≥ 2 or if μ has bounded density. This establishes that the minimization over parameterized curves is equivalent to minimizing over embedded curves and thus confirms that the problem has a geometric interpretation.
Mathematics Subject Classification: 49Q20 / 49K10 / 49Q10 / 35B65
Key words: Average-distance problem / principal curves / nonlocal variational problems
© EDP Sciences, SMAI 2016
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.