| Issue |
ESAIM: COCV
Volume 14, Number 3, July-September 2008
|
|
|---|---|---|
| Page(s) | 494 - 516 | |
| DOI | https://doi.org/10.1051/cocv:2007064 | |
| Published online | 21 December 2007 | |
A class of minimum principles for characterizing the trajectories and the relaxation of dissipative systems
1
Weierstraß-Institut für Angewandte Analysis und Stochastik, Mohrenstraße 39, 10117 Berlin, Germany; mielke@wias-berlin.de
2
Institut für Mathematik, Humboldt-Universität zu Berlin,
Rudower Chaussee 25, 12489 Berlin (Adlershof), Germany.
3
Division of Engineering and Applied Science,
California Institute of Technology,
Pasadena, CA 91125, USA.
Received:
20
May
2006
Revised:
31
October
2006
This work is concerned with the reformulation of evolutionary problems in a
weak form enabling consideration of solutions that may exhibit
evolving microstructures. This reformulation is accomplished by
expressing the evolutionary problem in variational form, i.e., by
identifying a functional whose minimizers represent entire
trajectories of the system. The particular class of functionals under
consideration is derived by first defining a sequence of time-discretized
minimum problems and subsequently formally passing to the limit of
continuous time. The resulting functionals may be regarded as a
weighted dissipation-energy functional with a weight decaying with a
rate 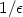 . The corresponding Euler-Lagrange equation leads to an
elliptic regularization of the original evolutionary problem. The
Γ-limit of these functionals for
. The corresponding Euler-Lagrange equation leads to an
elliptic regularization of the original evolutionary problem. The
Γ-limit of these functionals for 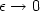 is highly
degenerate and provides limited
information regarding the limiting trajectories of the system. Instead we
seek to characterize the minimizing trajectories directly. The special class
of problems characterized by a rate-independent dissipation
functional is amenable to a particularly illuminating analysis. For these
systems it is possible to derive a priori bounds that are independent
of the regularizing parameter, whence it is possible to extract convergent
subsequences and find the limiting trajectories. Under general assumptions
on the functionals, we show that all such limits satisfy the energetic
formulation (S) & (E) for rate-independent systems. Moreover, we show
that the accumulation points of the regularized solutions solve the
associated limiting energetic formulation.
is highly
degenerate and provides limited
information regarding the limiting trajectories of the system. Instead we
seek to characterize the minimizing trajectories directly. The special class
of problems characterized by a rate-independent dissipation
functional is amenable to a particularly illuminating analysis. For these
systems it is possible to derive a priori bounds that are independent
of the regularizing parameter, whence it is possible to extract convergent
subsequences and find the limiting trajectories. Under general assumptions
on the functionals, we show that all such limits satisfy the energetic
formulation (S) & (E) for rate-independent systems. Moreover, we show
that the accumulation points of the regularized solutions solve the
associated limiting energetic formulation.
Mathematics Subject Classification: 49J40 / 49M20 / 49S05 / 74N10
Key words: Weighted energy-dissipation functional / incremental minimization problems / relaxation of evolutionary problems / rate-independent processes / energetic solutions
© EDP Sciences, SMAI, 2007
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


