| Issue |
ESAIM: COCV
Volume 14, Number 4, October-December 2008
|
|
|---|---|---|
| Page(s) | 725 - 743 | |
| DOI | https://doi.org/10.1051/cocv:2008005 | |
| Published online | 18 January 2008 | |
On some optimal control problems governed by a state equation with memory
Université Paris Dauphine, CEREMADE, Pl. de Lattre de Tassigny, 75775 Paris Cedex 16, France; carlier@ceremade.dauphine.fr; tahraoui@ceremade.dauphine.fr
Received:
17
October
2006
Revised:
20
March
2007
The aim of this paper is to study problems of the form:
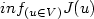with 
where V is a set of admissible controls and yu is the solution of the Cauchy problem:
, 
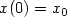and each 
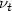is a nonnegative measure with support in [0,t]. After studying the Cauchy problem, we establish existence of minimizers, optimality conditions (in particular in the form of a nonlocal version of the Pontryagin principle) and prove some regularity results. We also consider the more general case where the control also enters the dynamics in a nonlocal way.
Mathematics Subject Classification: 34K35 / 49K25
Key words: Optimal control / memory
© EDP Sciences, SMAI, 2008
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.