| Issue |
ESAIM: COCV
Volume 15, Number 1, January-March 2009
|
|
|---|---|---|
| Page(s) | 68 - 101 | |
| DOI | https://doi.org/10.1051/cocv:2008067 | |
| Published online | 23 January 2009 | |
On the lower semicontinuous quasiconvex envelope for unbounded integrands (I)
Brandenburg University of Technology, Cottbus; Department of Mathematics, P.O.B. 10 13 44, 03013 Cottbus, Germany. e-mail: wagner@math.tu-cottbus.de
Received:
30
August
2006
Revised:
19
June
2007
Revised:
23
October
2007
Motivated by the study of multidimensional control problems of Dieudonné-Rashevsky type, we raise the question how to understand to notion of quasiconvexity for a continuous function f with a convex body K  instead of the whole space
instead of the whole space  as the range of definition. In the present paper, we trace the consequences of an infinite extension of f outside K, and thus study quasiconvex functions which are allowed to take the value +∞. As an appropriate envelope, we introduce and investigate the lower semicontinuous quasiconvex envelope
as the range of definition. In the present paper, we trace the consequences of an infinite extension of f outside K, and thus study quasiconvex functions which are allowed to take the value +∞. As an appropriate envelope, we introduce and investigate the lower semicontinuous quasiconvex envelope
 quasiconvex and lower semicontinuous,
quasiconvex and lower semicontinuous,
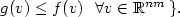 Our main result is a representation theorem for
Our main result is a representation theorem for  which generalizes Dacorogna's well-known theorem on the representation of the quasiconvex envelope of a finite function. The paper will be completed by the calculation of
which generalizes Dacorogna's well-known theorem on the representation of the quasiconvex envelope of a finite function. The paper will be completed by the calculation of  in two examples.
in two examples.
Mathematics Subject Classification: 26B25 / 26B40 / 49J45 / 52A20
Key words: Unbounded function / quasiconvex function / quasiconvex envelope / Morrey's integral inequality / representation theorem
© EDP Sciences, SMAI, 2008
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


