| Issue |
ESAIM: COCV
Volume 21, Number 4, October-December 2015
|
|
|---|---|---|
| Page(s) | 1053 - 1075 | |
| DOI | https://doi.org/10.1051/cocv/2014058 | |
| Published online | 24 June 2015 | |
On the lower semicontinuity of supremal functional under differential constraints
1
Dip. di Matematica, Sapienza Università di Roma, P.le Aldo Moro
2, 00185
Rome,
Italy.
ansini@mat.uniroma1.it
2
Department of Mathematical Sciences, University of
Bath, Claverton
Down, Bath,
BA2 7AY,
UK
3
Dip. di Matematica e Informatica, Università di
Ferrara, Via Machiavelli
35, 44121
Ferrara, Italy.
prnfnc1@unife.it
Received:
5
May
2014
We study the weak* lower semicontinuity of functionals of the form
where
Ω ⊂
ℝN is a bounded open set,
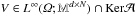 and 𝒜 is a constant-rank partial differential operator. The
notion of 𝒜-Young quasiconvexity, which is introduced here,
provides a sufficient condition when f(x,·) is only lower
semicontinuous. We also establish necessary conditions for weak* lower semicontinuity.
Finally, we discuss the divergence and curl-free cases and, as an application, we
characterise the strength set in the context of electrical resistivity.
and 𝒜 is a constant-rank partial differential operator. The
notion of 𝒜-Young quasiconvexity, which is introduced here,
provides a sufficient condition when f(x,·) is only lower
semicontinuous. We also establish necessary conditions for weak* lower semicontinuity.
Finally, we discuss the divergence and curl-free cases and, as an application, we
characterise the strength set in the context of electrical resistivity.
Mathematics Subject Classification: 49J45 / 35E99
Key words: Supremal functionals / Γ-convergence / Lp-approximation / lower semicontinuity / 𝒜-quasiconvexity
© EDP Sciences, SMAI 2015
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.