| Issue |
ESAIM: COCV
Volume 15, Number 1, January-March 2009
|
|
|---|---|---|
| Page(s) | 1 - 48 | |
| DOI | https://doi.org/10.1051/cocv:2008017 | |
| Published online | 23 January 2009 | |
Aubry sets and the differentiability of the minimal average action in codimension one
Dipartimento di Matematica,
Università Roma Tre, Largo S.
Leonardo Murialdo, 00146 Roma, Italy. bessi@matrm3.mat.uniroma3.it
Received:
3
November
2006
Revised:
23
July
2007
Let 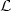 (x,u,∇u) be a Lagrangian periodic of period 1 in
x1,...,xn,u. We shall study the non self intersecting
functions u: Rn
(x,u,∇u) be a Lagrangian periodic of period 1 in
x1,...,xn,u. We shall study the non self intersecting
functions u: Rn R minimizing
R minimizing 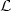 ; non self intersecting means that, if u(x0 + k) + j = u(x0)
for some x0 ∈ R n and (k , j) ∈ Z n × Z, then
u(x) = u(x + k) + j
; non self intersecting means that, if u(x0 + k) + j = u(x0)
for some x0 ∈ R n and (k , j) ∈ Z n × Z, then
u(x) = u(x + k) + j 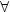 x. Moser has shown that each of these
functions is at finite distance from a plane
u = ρ
x. Moser has shown that each of these
functions is at finite distance from a plane
u = ρ  x and thus
has an average slope ρ; moreover, Senn has proven that it is
possible to define the average action of u, which is usually called
x and thus
has an average slope ρ; moreover, Senn has proven that it is
possible to define the average action of u, which is usually called 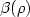 since it only depends on the slope of u.
Aubry and Senn have noticed a connection between
since it only depends on the slope of u.
Aubry and Senn have noticed a connection between 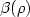 and the
theory of crystals in
and the
theory of crystals in  , interpreting
, interpreting 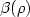 as the energy per area of a crystal face normal to
as the energy per area of a crystal face normal to 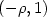 . The polar of β is usually called -α; Senn has shown that α is C1 and that the dimension of the flat of α which contains c depends only on the “rational space” of
. The polar of β is usually called -α; Senn has shown that α is C1 and that the dimension of the flat of α which contains c depends only on the “rational space” of  (c). We prove a similar result for the faces (or the faces of the faces, etc.) of the flats of α: they are C1 and their dimension depends only on the rational space of their normals.
(c). We prove a similar result for the faces (or the faces of the faces, etc.) of the flats of α: they are C1 and their dimension depends only on the rational space of their normals.
Mathematics Subject Classification: 35J20 / 35J60
Key words: Aubry-Mather theory for elliptic problems / corners of the mean average action
© EDP Sciences, SMAI, 2008
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


