| Issue |
ESAIM: COCV
Volume 11, Number 4, October 2005
|
|
|---|---|---|
| Page(s) | 633 - 672 | |
| DOI | https://doi.org/10.1051/cocv:2005023 | |
| Published online | 15 September 2005 | |
Entire solutions in
for a class of Allen-Cahn equations
Dipartimento di Scienze
Matematiche, Università Politecnica delle Marche, via
Brecce Bianche, 60131 Ancona, Italy; alessio@dipmat.univpm.it;montecch@mta01.univpm.it
Received:
10
September
2004
We consider a class of
semilinear elliptic equations of the form
15.7cm
-
where 
, 
is a periodic, positive function and
is modeled on the classical two well Ginzburg-Landau
potential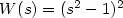 
. We look for solutions to ([see full textsee full text])
which verify the
asymptotic conditions 
as 
uniformly with respect to 
.
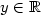We show via variational
methods that if ε is sufficiently small and a is not constant,
then ([see full textsee full text])
admits infinitely many of such solutions, distinct up to translations,
which do not exhibit one dimensional symmetries.
Mathematics Subject Classification: 34C37 / 35B05 / 35B40 / 35J20 / 35J60
Key words: Heteroclinic solutions / elliptic equations / variational methods.
© EDP Sciences, SMAI, 2005
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.