| Issue |
ESAIM: COCV
Volume 15, Number 2, April-June 2009
|
|
|---|---|---|
| Page(s) | 322 - 366 | |
| DOI | https://doi.org/10.1051/cocv:2008039 | |
| Published online | 24 June 2008 | |
The regularisation of the N-well problem by finite elements and by singular perturbation are scaling equivalent in two dimensions
MIS MPG, Inselstrasse 22,
04103 Leipzig, Germany. andrew.lorent@sns.it
Received:
7
June
2007
Revised:
15
January
2008
Let 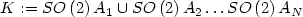 where
where  are matrices of non-zero determinant. We
establish a sharp relation between the following two minimisation
problems in two dimensions. Firstly the N-well problem with surface energy. Let
are matrices of non-zero determinant. We
establish a sharp relation between the following two minimisation
problems in two dimensions. Firstly the N-well problem with surface energy. Let
![$p\in\left[1,2\right]$](/articles/cocv/abs/2009/02/cocv0734/cocv0734_tex_eq3.png) ,
,  be a convex polytopal region. Define
be a convex polytopal region. Define
 and let AF denote the subspace of functions in
and let AF denote the subspace of functions in
 that satisfy the affine boundary condition
Du=F on
that satisfy the affine boundary condition
Du=F on  (in the sense of trace), where
(in the sense of trace), where  . We consider the scaling (with respect to ϵ) of
. We consider the scaling (with respect to ϵ) of
 Secondly the finite element approximation to the N-well problem
without surface energy. We will show there exists a space of functions
Secondly the finite element approximation to the N-well problem
without surface energy. We will show there exists a space of functions  where
each function
where
each function  is piecewise affine on a regular
(non-degenerate) h-triangulation and satisfies the affine boundary
condition v=lF on
is piecewise affine on a regular
(non-degenerate) h-triangulation and satisfies the affine boundary
condition v=lF on  (where lF is affine with
(where lF is affine with
 ) such that for
) such that for
 there exists positive constants
there exists positive constants  (depending on
(depending on
 , p) for which the following holds true
, p) for which the following holds true

Mathematics Subject Classification: 74N15
Key words: Two wells / surface energy
© EDP Sciences, SMAI, 2008
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


