| Issue |
ESAIM: COCV
Volume 16, Number 4, October-December 2010
|
|
|---|---|---|
| Page(s) | 1002 - 1017 | |
| DOI | https://doi.org/10.1051/cocv/2009030 | |
| Published online | 11 August 2009 | |
A regularity result for a convex functional and bounds for the singular set
Dipartimento di Matematica e Applicazioni “R. Caccioppoli” Università
di Napoli “Federico II” Via Cintia, 80126 Napoli, Italy. bruno.demaria@dma.unina.it
Received:
4
February
2009
Revised:
6
May
2009
In this paper we prove a regularity result for local minimizers of functionals of the Calculus of Variations of the type
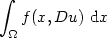
where Ω is a bounded open set in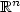 
, u ∈ 
(Ω; 
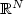), p > 1, n ≥ 2 and N ≥ 1.
We use the technique of difference quotient without the usual assumption on the growth of the second derivatives of the function f. We apply this result to give
a bound on the Hausdorff dimension of the singular set of minimizers.
Mathematics Subject Classification: 35J50 / 35J60 / 35B65
Key words: Partial regularity / singular sets / fractional differentiability / variational integrals
© EDP Sciences, SMAI, 2009
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.