An a priori Campanato type regularity condition for local minimisers in the calculus of variations

Thomas J. Dodd

doi:10.1051/cocv:2008066

All issues

Volume 16 / No 1 (January-March 2010)

ESAIM: COCV, 16 1 (2010) 111-131

Abstract

Free Access

Issue		ESAIM: COCV Volume 16, Number 1, January-March 2010


Page(s)		111 - 131
DOI		https://doi.org/10.1051/cocv:2008066
Published online		21 October 2008

ESAIM: COCV 16 (2010) 111-131

An a priori Campanato type regularity condition for local minimisers in the calculus of variations

Thomas J. Dodd

Department of Mathematics and the Maxwell Institute for Mathematical Sciences, Heriot-Watt University, Riccarton, Edinburgh EH14 4AS, UK. T.J.Dodd@ma.hw.ac.uk

Received: 28 April 2008

Abstract

An a priori Campanato type regularity condition is established for a class of W¹X local minimisers $\overline{u}$ of the general variational integral $\int_{\Omega} F(\nabla u(x))\,{\rm d}x$ where $\Omega \subset \mathbb{R}^n$ is an open bounded domain, F is of class C², F is strongly quasi-convex and satisfies the growth condition $F(\xi)\leq c(1+|\xi|^p)$ for a p > 1 and where the corresponding Banach spaces X are the Morrey-Campanato space $\mathcal{L}^{p,\mu} (\Omega,\mathbb{R}^{N\times n})$ , µ < n, Campanato space $\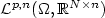mathcal{L}^{p,n}(\Omega,\mathbb{R}^{N\times n})$ and the space of bounded mean oscillation ${\rm BMO} \Omega,\mathbb{R}^{N\times n})$ . The admissible maps $u\colon \Omega \to \mathbb{R}^N$ are of Sobolev class W^1,p, satisfying a Dirichlet boundary condition, and to help clarify the significance of the above result the sufficiency condition for W¹BMO local minimisers is extended from Lipschitz maps to this admissible class.

Mathematics Subject Classification: 49N60 / 49K10

Key words: Calculus of variations / local minimiser / partial regularity / strong quasiconvexity / Campanato space / Morrey space / Morrey-Campanato space / space of bounded mean oscillation / extremals / positive second variation

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.