| Issue |
ESAIM: COCV
Volume 16, Number 2, April-June 2010
|
|
|---|---|---|
| Page(s) | 327 - 336 | |
| DOI | https://doi.org/10.1051/cocv:2008072 | |
| Published online | 19 December 2008 | |
Uniqueness of solutions for some elliptic equations with a quadratic gradient term
1
Departamento de Análisis Matemático,
Universidad de Granada,
Campus Fuentenueva s/n, 18071 Granada, Spain. darcoya@ugr.es
2
Departament d'Anàlisi Matemàtica,
Universitat de València, Dr. Moliner 50, 46100 Burjassot,
Valencia, Spain. sergio.segura@uv.es
Received:
27
May
2008
Revised:
2
October
2008
We study a comparison principle and uniqueness of positive solutions for the homogeneous Dirichlet boundary value problem associated to quasi-linear elliptic equations with lower order terms. A model example is given by
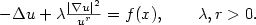
The main feature of these equations consists in having a quadratic gradient term in which singularities are allowed. The arguments employed here also work to deal with equations having lack of ellipticity or some dependence on u in the right hand side. Furthermore, they could be applied to obtain uniqueness results for nonlinear equations having the p-Laplacian operator as the principal part. Our results improve those already known, even if the gradient term is not singular.
Mathematics Subject Classification: 35J65 / 35J70 / 35J60
Key words: Non linear elliptic problems / uniqueness / comparison principle / lower order terms with singularities at the Gradient term / lack of coerciveness
© EDP Sciences, SMAI, 2008
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


