| Issue |
ESAIM: COCV
Volume 17, Number 4, October-December 2011
|
|
|---|---|---|
| Page(s) | 1066 - 1087 | |
| DOI | https://doi.org/10.1051/cocv/2010037 | |
| Published online | 28 October 2010 | |
Estimate of the pressure when its gradient is the divergence of a measure. Applications
1
Institut de Recherche Mathématique de Rennes, INSA de Rennes, France. mbriane@insa-rennes.fr
2
Dpto. de Ecuaciones Diferenciales y Análisis Numérico, Universidad de Sevilla, Spain. jcasadod@us.es
Received:
22
February
2010
Revised:
28
April
2010
In this paper, a 
estimate of the pressure is derived when its gradient is the divergence of a matrix-valued measure on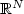 
, or on a regular bounded open set of 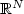. The proof is based partially on the Strauss inequality [Strauss, Partial Differential Equations: Proc. Symp. Pure Math. 23 (1973) 207–214] in dimension two, and on a recent result of Bourgain and Brezis [J. Eur. Math. Soc. 9 (2007) 277–315] in higher dimension. The estimate is used to derive a representation result for divergence free distributions which read as the divergence of a measure, and to prove an existence result for the stationary Navier-Stokes equation when the viscosity tensor is only in L1.
Mathematics Subject Classification: 35Q30 / 35Q35 / 35A08
Key words: Pressure / Navier-Stokes equation / div-curl / measure data / fundamental solution
© EDP Sciences, SMAI, 2010
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.