| Issue |
ESAIM: COCV
Volume 15, Number 4, October-December 2009
|
|
|---|---|---|
| Page(s) | 818 - 838 | |
| DOI | https://doi.org/10.1051/cocv:2008048 | |
| Published online | 19 July 2008 | |
A characterization of gradient Young-concentration measures generated by solutions of Dirichlet-type problems with large sources
1
LMAH (Laboratoire de Mathématiques Appliquées du Havre), Université du Havre, 25 rue Philippe Lebon, BP 540, 76058 Le Havre, France.
gisella.croce@univ-lehavre.fr
2
I3M (Institut de Mathématiques et de Modélisation de Montpellier), UMR-CNRS 5149, Université Montpellier II, Case courrier 051, Place Eugène Bataillon, 34095 Montpellier Cedex 5, France. lacour@math.univ-montp2.fr
3
EMIAN, Université de Nîmes, France. micha@math.univ-montp2.fr
Received:
7
January
2008
We show how to capture the gradient concentration of the solutions of Dirichlet-type
problems subjected to large sources of order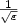 
concentrated on an ε-neighborhood of a hypersurface of the domain. To this end we define the
gradient Young-concentration measures generated by sequences of finite energy and establish a very simple
characterization of these measures.
Mathematics Subject Classification: 49Q20 / 28A33
Key words: Gradient Young measures / concentration measures / minimization problems / quasiconvexity
© EDP Sciences, SMAI, 2008
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.