| Issue |
ESAIM: COCV
Volume 20, Number 1, January-March 2014
|
|
|---|---|---|
| Page(s) | 1 - 22 | |
| DOI | https://doi.org/10.1051/cocv/2013050 | |
| Published online | 29 August 2013 | |
Shape optimization problems for metric graphs
1
Dipartimento di Matematica, Università di Pisa,
Largo B. Pontecorvo 5,
56127
Pisa,
Italy
buttazzo@dm.unipi.it
2
Scuola Normale Superiore di Pisa, Piazza dei Cavalieri 7, 56126
Pisa,
Italy
berardo.ruffini@sns.it; b.velichkov@sns.it
Received:
20
September
2012
Revised:
18
December
2012
We consider the shape optimization problem
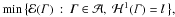where ℋ1 is the one-dimensional Hausdorff
measure and 𝒜 is an admissible class of one-dimensional sets
connecting some prescribed set of points 
. The cost functional ℰ(Γ) is the
Dirichlet energy of Γ defined through the Sobolev functions on
Γ vanishing on the points
Di. We analyze the existence of a solution
in both the families of connected sets and of metric graphs. At the end, several explicit
examples are discussed.
Mathematics Subject Classification: 49R05 / 49Q20 / 49J45 / 81Q35
Key words: Shape optimization / rectifiable sets / metric graphs / quantum graphs / Dirichlet energy
© EDP Sciences, SMAI, 2013
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.