Regularity analysis for an abstract thermoelastic system with inertial term

¹ Computer Science Department, Stanford University, Stanford, CA 94305, USA.
² Department of Mathematics and Statistics, University of Minnesota, Duluth, MN 55812-2496, USA.
³ School of Mathematics, Beijing Institute of Technology, P.R. China.
⁴ Department of Mathematics, Federal University of Juiz de Fora, CEP 36036-900, Juiz de Fora, MG, Brazil.

^* Corresponding author: zliu@d.umn.edu

Received: 3 June 2020
Accepted: 5 November 2020

Abstract

In this paper, we provide a complete regularity analysis for the following abstract thermoelastic system with inertial term

$\{\\ \\ \rho u_{\mathrm{tt}}+l{A}^{\gamma }{u}_{\mathrm{tt}}+\mathrm{\sigma Au}-m{A}^{\alpha }\theta & =0,\\ \\ \\ c{\theta }_t+m{A}^{\alpha }{u}_t+k{A}^{\beta }\theta & =0,\\ \\ \\ u\left(0\right)=u_0,u_t\left(0\right)=v_0,& \theta \left(0\right)={\theta }_0,$

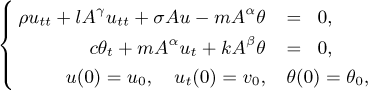
where A is a self-adjoint, positive definite operator on a complex Hilbert space H and

$\left(\alpha ,\beta ,\gamma \right)\in E=\left[0,\frac{\beta +1}{2}\right]\times \left[0,1\right]\times \left[0,1\right].$

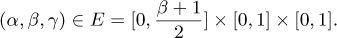
It is regarded as the second part of Fernández Sare et al. [J. Diff. Eqs. 267 (2019) 7085–7134]. where the asymptotic stability of this model was investigated. We are able to decompose the region E into three parts where the associated semigroups are analytic, of Gevrey classes of specific order, and non-smoothing, respectively. Moreover, by a detailed spectral analysis, we will show that the orders of Gevrey class are sharp, under proper conditions. We also show that the orders of polynomial stability obtained in Fernández Sare et al. [J. Diff. Eqs. 267 (2019) 7085–7134] are optimal.