| Issue |
ESAIM: COCV
Volume 27, 2021
|
|
|---|---|---|
| Article Number | 38 | |
| Number of page(s) | 37 | |
| DOI | https://doi.org/10.1051/cocv/2021042 | |
| Published online | 30 April 2021 | |
Linear convergence of accelerated conditional gradient algorithms in spaces of measures*
1
Computer Science and Mathematics Division, Oak Ridge National Laboratory, One Bethel Valley Road, P.O. Box 2008, MS-6211,
Oak Ridge,
TN
37831, USA.
2
Johann Radon Institute for Computational and Applied Mathematics, ÖAW,
Altenbergerstraße 69,
4040
Linz, Austria.
** Corresponding author: daniel.walter@oeaw.ac.at
Received:
26
November
2019
Accepted:
9
April
2021
A class of generalized conditional gradient algorithms for the solution of optimization problem in spaces of Radon measures is presented. The method iteratively inserts additional Dirac-delta functions and optimizes the corresponding coefficients. Under general assumptions, a sub-linear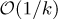 
rate in the objective functional is obtained, which is sharp in most cases. To improve efficiency, one can fully resolve the finite-dimensional subproblems occurring in each iteration of the method. We provide an analysis for the resulting procedure: under a structural assumption on the optimal solution, a linear 
convergence rate is obtained locally.
Mathematics Subject Classification: 46E27 / 65J22 / 65K05 / 90C25 / 49M05
Key words: Vector-valued finite Radon measures / generalized conditional gradient / sparsity / nonsmooth optimization
KP acknowledges funding by the US Air Force Office of Scientific Research grant FA9550-15-1-0001 and the Laboratory Directed Research and Development Program at Oak Ridge National Laboratory (ORNL), managed by UT-Battelle, LLC, under Contract No. DE-AC05-00OR22725 with the US Department of Energy (DOE). The US government retains and the publisher, by accepting the article for publication, acknowledges that the US government retains a nonexclusive, paid-up, irrevocable, worldwide license to publish or reproduce the published form of this manuscript, or allow others to do so, for US government purposes. DOE will provide public access to these results of federally sponsored research in accordance with the DOE Public Access Plan (http://energy.gov/downloads/doe-public-access-plan). DW acknowledges support by the DFG through the International Research Training Group IGDK 1754 “Optimization and Numerical Analysis for Partial Differential Equations with Nonsmooth Structures”. Furthermore, support from the TopMath Graduate Center of TUM Graduate School at Technische Universität München, Germany and from the TopMath Program at the Elite Network of Bavaria is gratefully acknowledged.
© EDP Sciences, SMAI 2021
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.