| Issue |
ESAIM: COCV
Volume 27, 2021
|
|
|---|---|---|
| Article Number | 18 | |
| Number of page(s) | 29 | |
| DOI | https://doi.org/10.1051/cocv/2020090 | |
| Published online | 22 March 2021 | |
A minimizing Movement approach to a class of scalar reaction–diffusion equations
Technische Universität München,
München, Germany.
* Corresponding author: fleissne@ma.tum.de
Received:
11
February
2020
Accepted:
15
December
2020
The purpose of this paper is to introduce a Minimizing Movement approach to scalar reaction–diffusion equations of the form

with parameters Λ, Σ > 0 and no-flux boundary condition
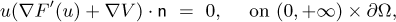
which is built on their gradient-flow-like structure in the space  of finite nonnegative Radon measures on
of finite nonnegative Radon measures on  , endowed with the recently introduced Hellinger-Kantorovich distance HKΛ,Σ. It is proved that, under natural general assumptions on
, endowed with the recently introduced Hellinger-Kantorovich distance HKΛ,Σ. It is proved that, under natural general assumptions on  and
and  , the Minimizing Movement scheme
, the Minimizing Movement scheme

yields weak solutions to the above equation as the discrete time step size τ ↓ 0. Moreover, a superdifferentiability property of the Hellinger-Kantorovich distance HKΛ,Σ, which will play an important role in this context, is established in the general setting of a separable Hilbert space; that result will constitute a starting point for the study of the differentiability of HKΛ,Σ along absolutely continuous curves which will be carried out in a subsequent paper.
Mathematics Subject Classification: 35K57 / 35K20 / 35K55 / 49M25 / 47J25 / 47J30 / 28A33 / 54E35 / 46G99 / 49Q20
Key words: Optimal transport / gradient flows / Minimizing Movements / reactiondiffusion equations / Hellinger-Kantorovich distance
© EDP Sciences, SMAI 2021
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



