| Issue |
ESAIM: COCV
Volume 29, 2023
|
|
|---|---|---|
| Article Number | 12 | |
| Number of page(s) | 20 | |
| DOI | https://doi.org/10.1051/cocv/2022079 | |
| Published online | 19 January 2023 | |
Uniform boundedness for the optimal controls of a discontinuous, non-convex Bolza problem*,, **
1
Univ Brest, UMR CNRS 6205, Laboratoire de Mathématiques de Bretagne Atlantique,
6 Avenue Victor Le Gorgeu,
Brest
29200,
France
2
Università degli Studi di Padova, Dipartimento di Matematica “Tullio Levi-Civita”,
Via Trieste 63,
35121
Padova,
Italy
*** Corresponding author: carlo.mariconda@unipd.it
Received:
23
July
2021
Accepted:
25
November
2022
We consider a Bolza type optimal control problem of the form

Subject to:
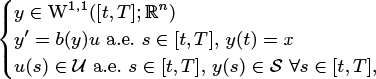
where Λ(s, y, u) is locally Lipschitz in s, just Borel in (y, u), b has at most a linear growth and both the Lagrangian Λ and the end-point cost function g may take the value +∞. If b ≡ 1, g ≡ 0, (Pt, x) is the classical problem of the Calculus of Variations. We suppose the validity of a slow growth condition in u, introduced by Clarke in 1993, including Lagrangians of the type
 and
and
 and the superlinear case. We show that, if Λ is real valued, any family of optimal pairs (y*, u*) for (Pt,x) whose energy Jt(y*, u*) is equi-boundcd as (t, x) vary in a compact set, has L∞ – equibounded controls. Moreover, if Λ is extended valued, the same conclusion holds under an additional lower semicontinuity assumption on (s, u) ↦ Λ(s, y, u) and requiring a condition on the structure of the effective domain. No convexity, nor local Lipschitzianity is assumed on the variables (y, u). As an application we obtain the local Lipschitz continuity of the value function under slow growth assumptions.
and the superlinear case. We show that, if Λ is real valued, any family of optimal pairs (y*, u*) for (Pt,x) whose energy Jt(y*, u*) is equi-boundcd as (t, x) vary in a compact set, has L∞ – equibounded controls. Moreover, if Λ is extended valued, the same conclusion holds under an additional lower semicontinuity assumption on (s, u) ↦ Λ(s, y, u) and requiring a condition on the structure of the effective domain. No convexity, nor local Lipschitzianity is assumed on the variables (y, u). As an application we obtain the local Lipschitz continuity of the value function under slow growth assumptions.
Mathematics Subject Classification: 49N60 / 49K05 / 90C25
Key words: Regularity / Lipschitz / uniform / growth
© The authors. Published by EDP Sciences, SMAI 2023
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


