| Issue |
ESAIM: COCV
Volume 5, 2000
|
|
|---|---|---|
| Page(s) | 71 - 85 | |
| DOI | https://doi.org/10.1051/cocv:2000102 | |
| Published online | 15 August 2002 | |
Relaxation of singular functionals defined on Sobolev spaces
1
Département de Mathématiques,
Institut Préparatoire aux Études d'Ingénieurs de
Sfax, Route Menzel Chaker - Km 0,5, BP. 805, 3000 Sfax,
Tunisia; Fax: (00-216) 4. 246. 347.
2
Max-Planck Institute for Mathematics in the Sciences,
Inselstr. 22-26, 04103 Leipzig, Germany; Hafedh.Belgacem@mis.mpg.de.
Received:
1
December
1998
Revised:
17
November
1999
In this paper, we consider a Borel
measurable function on
the space of
 matrices
matrices  taking the value
taking the value
 , such that its rank-one-convex
envelope
, such that its rank-one-convex
envelope
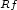 is finite and satisfies for some fixed
is finite and satisfies for some fixed
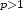 :
:
 where
where
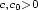 . Let
. Let  be a given
regular bounded
open domain of
be a given
regular bounded
open domain of
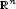 . We define on
. We define on 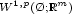 the functional
the functional
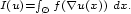 Then, under some technical restrictions on
Then, under some technical restrictions on
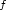 , we show that the relaxed functional
, we show that the relaxed functional
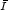 for the weak topology
of
for the weak topology
of
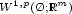 has the integral
representation:
has the integral
representation:
)\ dx,$$](/articles/cocv/abs/2000/01/cocvVol5-3/cocvVol5-3_tex_eq15.png) where for a given function
where for a given function  ,
,
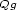 denotes its
quasiconvex envelope.
denotes its
quasiconvex envelope.
Résumé
On considère une fonction Borel mesurable
 qui prend la valeur
qui prend la valeur
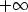 , dont l'enveloppe
rang-1-convexe Rf est finie et satisfait pour un certain p>1,
, dont l'enveloppe
rang-1-convexe Rf est finie et satisfait pour un certain p>1, 
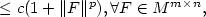 avec
avec  fixés. Étant donné un ouvert borné Ω de
fixés. Étant donné un ouvert borné Ω de 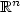 , on introduit
la
fonctionnelle
, on introduit
la
fonctionnelle 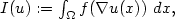 pour
pour 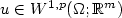 . On montre alors sous quelques hypothèses
supplémentaires concernant f, que la relaxée
. On montre alors sous quelques hypothèses
supplémentaires concernant f, que la relaxée 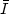 de I
pour la topolgie faible de
de I
pour la topolgie faible de  admet la représentation
suivante :
admet la représentation
suivante : 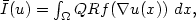 où pour une
fonction donnée g, Qg désigne son enveloppe quasi-convexe.
où pour une
fonction donnée g, Qg désigne son enveloppe quasi-convexe.
Mathematics Subject Classification: 49-xx
Key words: Rank-one convexity / quasiconvexity / weak lower semicontinuity.
© EDP Sciences, SMAI, 2000
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


