| Issue |
ESAIM: COCV
Volume 6, 2001
|
|
|---|---|---|
| Page(s) | 593 - 611 | |
| DOI | https://doi.org/10.1051/cocv:2001124 | |
| Published online | 15 August 2002 | |
On the existence of nonsmooth control-Lyapunov functions in the sense of generalized gradients
Institut Girard Desargues, Université
Claude Bernard Lyon I, 69622 Villeurbanne, France; rifford@desargues.univ-lyon1.fr.
Received:
21
August
2000
Revised:
2
May
2001
Let 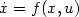 be a general control system; the existence of a
smooth control-Lyapunov function does not imply the existence of a continuous
stabilizing feedback. However, we show that it allows us to design a
stabilizing feedback in the Krasovskii (or Filippov) sense. Moreover,
we recall a definition of a control-Lyapunov function
in the case of a nonsmooth function; it is based on Clarke's
generalized gradient. Finally, with an inedite proof we prove that the existence of this type of control-Lyapunov function is equivalent to the existence of a
classical control-Lyapunov function. This property leads to a generalization
of a result on the systems with integrator.
be a general control system; the existence of a
smooth control-Lyapunov function does not imply the existence of a continuous
stabilizing feedback. However, we show that it allows us to design a
stabilizing feedback in the Krasovskii (or Filippov) sense. Moreover,
we recall a definition of a control-Lyapunov function
in the case of a nonsmooth function; it is based on Clarke's
generalized gradient. Finally, with an inedite proof we prove that the existence of this type of control-Lyapunov function is equivalent to the existence of a
classical control-Lyapunov function. This property leads to a generalization
of a result on the systems with integrator.
Mathematics Subject Classification: 93D05 / 93D15 / 93D20 / 93D30 / 93D09 / 93B05
Key words: Asymptotic stabilizability / converse Lyapunov theorem / nonsmooth analysis / differential inclusion / and Krasovskii solutions / feedback.
© EDP Sciences, SMAI, 2001
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


