| Issue |
ESAIM: COCV
Volume 10, Number 4, October 2004
|
|
|---|---|---|
| Page(s) | 624 - 633 | |
| DOI | https://doi.org/10.1051/cocv:2004023 | |
| Published online | 15 October 2004 | |
Anisotropic functions: a genericity result with crystallographic implications
1
Department of Mathematical Sciences,
Carnegie Mellon University, USA; Fagel@cmu.edu.
2
Department of Mathematics, Technion-Israel Institute of
Technology, 32000, Haifa, Israel; ajzasl@tx.technion.ac.il.
Received:
27
August
2003
In the 1950's and 1960's surface physicists/metallurgists such as
Herring and Mullins applied ingenious thermodynamic arguments to explain a
number of experimentally observed surface phenomena in crystals. These insights permitted
the successful engineering of a large number of alloys, where the
major mathematical novelty was that the surface response to external stress was anisotropic.
By examining step/terrace (vicinal) surface defects it was discovered through
lengthy and tedious experiments that the stored energy density (surface tension)
along a step edge was a smooth symmetric function β of the azimuthal angle θ to the
step, and that the positive function β attains its minimum value at  and its maximum value at
and its maximum value at  . The function β provided the crucial thermodynamic
parameters needed for the engineering of these materials. Moreover the minimal energy
configuration of the step is determined by the values of the stiffness function
. The function β provided the crucial thermodynamic
parameters needed for the engineering of these materials. Moreover the minimal energy
configuration of the step is determined by the values of the stiffness function 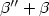 which ultimately leads to the magnitude and direction of surface mass flow for
these materials. In the 1990's there was a dramatic improvement in electron microscopy
which permitted real time observation of the meanderings of a step edge under
Brownian heat oscillations. These observations provided much more rapid
determination of the relevant thermodynamic parameters for the step edge, even for crystals at
temperatures below their roughening temperature. Use of these tools led J.
Hannon and his coexperimenters to discover that some crystals behave in a highly anti-intuitive
manner as their temperature is varied. The present article is devoted to
a model described by a class of variational problems. The main result of the paper
describes the solutions of the corresponding problem for a generic integrand.
which ultimately leads to the magnitude and direction of surface mass flow for
these materials. In the 1990's there was a dramatic improvement in electron microscopy
which permitted real time observation of the meanderings of a step edge under
Brownian heat oscillations. These observations provided much more rapid
determination of the relevant thermodynamic parameters for the step edge, even for crystals at
temperatures below their roughening temperature. Use of these tools led J.
Hannon and his coexperimenters to discover that some crystals behave in a highly anti-intuitive
manner as their temperature is varied. The present article is devoted to
a model described by a class of variational problems. The main result of the paper
describes the solutions of the corresponding problem for a generic integrand.
Mathematics Subject Classification: 49J99 / 26A21 / 82O25 / 74E15
Key words: Complete metric space / generic property / variational problem.
© EDP Sciences, SMAI, 2004
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


