| Issue |
ESAIM: COCV
Volume 13, Number 4, October-December 2007
|
|
|---|---|---|
| Page(s) | 735 - 749 | |
| DOI | https://doi.org/10.1051/cocv:2007030 | |
| Published online | 20 July 2007 | |
Homogenization of periodic non self-adjoint problems with large drift and potential
1
Centre de Mathématiques
Appliquées, École Polytechnique, 91128 Palaiseau Cedex, Paris, France; gregoire.allaire@polytechnique.fr
2
Departamento de Matemáticas, Universidad Autónoma de Madrid, 28049
Madrid, Spain; rafael.orive@uam.es
Received:
11
July
2005
Revised:
29
June
2006
We consider the homogenization of both the parabolic and eigenvalue problems for a singularly perturbed
convection-diffusion equation in a periodic medium. All coefficients of the equation may vary both on the
macroscopic scale and on the periodic microscopic scale. Denoting by ε the period, the potential or zero-order
term is scaled as  and the drift or first-order term is scaled as
and the drift or first-order term is scaled as 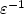 . Under a structural
hypothesis on the first cell eigenvalue, which is assumed to admit a unique minimum in the domain with
non-degenerate quadratic behavior, we prove an exponential localization at this minimum point. The homogenized
problem features a diffusion equation with quadratic potential in the whole space.
. Under a structural
hypothesis on the first cell eigenvalue, which is assumed to admit a unique minimum in the domain with
non-degenerate quadratic behavior, we prove an exponential localization at this minimum point. The homogenized
problem features a diffusion equation with quadratic potential in the whole space.
Mathematics Subject Classification: 35B27 / 35K57 / 35P15 / 74Q10
Key words: Homogenization / non self-adjoint operators / convection-diffusion / periodic medium
© EDP Sciences, SMAI, 2007
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


