| Issue |
ESAIM: COCV
Volume 21, Number 3, July-September 2015
|
|
|---|---|---|
| Page(s) | 670 - 689 | |
| DOI | https://doi.org/10.1051/cocv/2014043 | |
| Published online | 13 May 2015 | |
Magnetic spectral bounds on starlike plane domains
1
Department of Mathematics, University of Illinois,
Urbana, IL
61801,
USA
Laugesen@illinois.edu
2
Department of Mathematics, University of Oregon,
Eugene, OR
97403,
USA
Siudeja@uoregon.edu
Received:
5
January
2014
Revised:
3
June
2014
We develop sharp upper bounds for energy levels of the magnetic Laplacian on starlike
plane domains, under either Dirichlet or Neumann boundary conditions and assuming a
constant magnetic field in the transverse direction. Our main result says that
∑j=1n
Φ(λjA/G)
is maximal for a disk whenever Φ is concave increasing, n ≥ 1, the domain has area
A, and
λj is the
jth
Dirichlet eigenvalue of the magnetic Laplacian (i∇ +
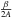 (−x2,x1))2.
Here the flux β is constant, and the scale invariant factor
G penalizes
deviations from roundness, meaning G ≥ 1 for all domains and G = 1 for disks.
(−x2,x1))2.
Here the flux β is constant, and the scale invariant factor
G penalizes
deviations from roundness, meaning G ≥ 1 for all domains and G = 1 for disks.
Mathematics Subject Classification: 35P15 / 35J20
Key words: Isoperimetric / spectral zeta / heat trace / partition function / Pauli operator
© EDP Sciences, SMAI, 2015
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


