EDP Sciences logo
Subscriber Authentication Point
Search
Menu
All issues Volume 5 (2000) ESAIM: COCV, 5 (2000) 445-475 References
Free Access
Issue
ESAIM: COCV
Volume 5, 2000
Page(s) 445 - 475
DOI https://doi.org/10.1051/cocv:2000117
Published online 15 August 2002
  1. R. Acart and C. Vogel, Analysis of bounded variation methods for ill-posed problems. Inverse Problems 10 (1994) 1217-1229. [CrossRef] [MathSciNet] [Google Scholar]
  2. H.C. Andrews and B.R. Hunt, Digital signal processing. Tech. Englewood Cliffs, NJ: Prentice-Hall (1977). [Google Scholar]
  3. S.M. Berman, Sojournes and Extremes os Stochastic Processes. Wadsworth, Reading, MA (1989). [Google Scholar]
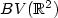  4. A. Cohen, R. De Vore, P. Petrushev and H. Xu, Nonlinear Approximation and the Space Formula (preprint). [Google Scholar]
  5. V. Caselles, J.L. Lisani, J.M. Morel and G. Sapiro, Shape Preserving Local Histogram Modification. IEEE Trans. Image Process. 8 (1999). [Google Scholar]
  6. A. Chambolle, R.A. De Vore, N. Lee and B.J. Lucier, Nonlinear Wavelet Image Processing: Variational Problems, Compression and Noise Removal through Wavelet Shrinkage. Preprint CEREMADE No. 9728, September 1997, short version in: IEEE Trans. Image Process. 7 (1998) 319-335. [Google Scholar]
  7. A. Chambolle and P.L. Lions, Restauration de données par minimisation de la variation Total et variantes d'ordre supérieur, in Proc. of GRETSI. Juan-les-Pins, France (1995). [Google Scholar]
  8. A. Chambolle and P.L. Lions, Image recovery via Total Variation minimisation and related problems. Numer. Math. 76 (1997) 167-188. IEEE Trans. Image Process. [CrossRef] [MathSciNet] [Google Scholar]
  9. R.H. Chan, T.F. Chan and C Wong, Cosine Transform Based Preconditioners for Total Variation Deblurring. UCLA Math Department CAM Report 95-23 (1995). [Google Scholar]
  10. R.R. Coifman and D.L. Donoho, Translation-invariant de-noising. Technical Report 475, Standford University (1995). [Google Scholar]
  11. R.R. Coifman, Y. Meyer and M.V. Wickerhauser, Wavelet analysis and signal processing. In Wavelets and their Applications, edited by B. Ruskai et al., Boston, Jones and Barlett (1992) 153-178. [Google Scholar]
  12. G. Demoment, Image reconstruction and restoration: Overview of Common Estimation Structures and Problems. IEEE Trans. Acoust. Speech Signal Process. 37 (1989). [Google Scholar]
  13. D. Donoho and I.M. Johnstone, Minimax Estimation via wavelet shrinkage. Tech. Report, Dept. of Stat., Stanford Univ. (1992). [Google Scholar]
  14. D.L. Donoho and I.M. Johnstone, Ideal spatial adaptation by wavelet shrinkage. Biometrika 81 (1994) 425-455. [CrossRef] [MathSciNet] [Google Scholar]
  15. L.C. Evans and R.F. Gariepy, Measure theory and fine properties of functions. Studies in advanced mathematics, CRS Press Inc. (1992). [Google Scholar]
  16. F. Guichard and F. Malgouyres, Total Variation Based interpolation, in Proc. of European Signal Processing Conference (EUSIPCO-98), Vol. 3 (1998) 1741-1744. [Google Scholar]
  17. I.M. Johnstone and B.W. Silverman, Wavelet threshold estimators for data with correlated noise. Technical report, Standford University (1994). [Google Scholar]
  18. T. Kailath, A View of Three Decades of Linear Filtering Theory. IEEE Trans. Inform. Theory IT20 (1974). [Google Scholar]
  19. J. Kalifa, Restauration minimax et déconvolution dans un base d'ondelettes miroirs. Thèse, École Polytechnique (1999). [Google Scholar]
  20. J. Kalifa, S. Mallat and B. Rougé, Restauration d'images par paquets d'ondelettes. 16e Colloque GRETSI (1997). [Google Scholar]
  21. J. Kalifa, S. Mallat and B. Rougé, Image Deconvolution in Mirror Wavelet Bases. IEEE, ICIP'98. [Google Scholar]
  22. H.J. Landau and H.O. Pollak, Prolate Speroidal Wave Functions, Fourier Analysis and Uncertainty -III: The Dimension of the Space of Essentially Time and Band-Limited Signals. The Bell systeme technical Journal (1962). [Google Scholar]
  23. M. Lindenbaum, M. Fischer and A. Bruckstein, On Gabor's contribution to image enhancement. PR. 27 (1994) 1-8. [Google Scholar]
  24. S. Mallat, A theory for multiresolution signal decomposition: The wavelet representation. IEEE Trans. Patern Analysis and Machine Intelligence II (1989). [Google Scholar]
  25. S. Mallat, A Wavelet Tour of Signal Processing. Academic Press (1998). [Google Scholar]
  26. Y. Meyer, Ondelettes et opérateurs. Hermann (1990) Tome 1. [Google Scholar]
  27. Y. Meyer, Les ondelettes, algorithmes et applications. Armand Colin (1992). [Google Scholar]
  28. M. Nikolova, Local strong homogeneity of a regularized estimator. SIAM (to appear). [Google Scholar]
  29. B. Rougé, Remarks about space-frequency and space-scale to clean and restore noisy images in satellite frameworks. Progress in wavelets and applications, edited by Y.Meyer and S. Roques Frontières. Gif-sur-Yvette 1993 (Proceedings Toulouse conference). [Google Scholar]
  30. B. Rougé, Fixed Chosen Noise Restauration (FCNR). IEEE 95 Philadelphia (U.S.A.). [Google Scholar]
  31. L. Rudin, S. Osher and E. Fatemi, Nonlinear Total Variation based noise removal algorithms. Physica D 60 (1992) 259-268. [Google Scholar]

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.