EDP Sciences logo
Subscriber Authentication Point
Search
Menu
All issues Volume 13 / No 3 (July-September 2007) ESAIM: COCV, 13 3 (2007) 458-483 References
Free Access
Issue
ESAIM: COCV
Volume 13, Number 3, July-September 2007
Page(s) 458 - 483
DOI https://doi.org/10.1051/cocv:2007022
Published online 05 June 2007
  1. H.T. Banks, R.C. Smith and Y. Wang, Smart Material Structures: Modeling, Estimation, Control. Masson, Paris (1996). [Google Scholar]
  2. M. Brokate, Hysteresis operators, in Phase Transitions and Hysteresis, A. Visintin Ed., Springer, Berlin (1994) 1–38. [Google Scholar]
  3. M. Brokate and J. Sprekels, Hysteresis and Phase Transitions, Springer, New York (1996). [Google Scholar]
  4. C.I. Byrnes, D.S. Gilliam, V.I. Shubov and G. Weiss, Regular linear systems governed by a boundary controlled heat equation. J. Dynam. Control Syst. 8 (2002) 341–370. [CrossRef] [Google Scholar]
  5. R.F. Curtain, H. Logemann and O. Staffans, Stability results of Popov-type for infinite-dimensional systems with applications to integral control. Proc. London Math. Soc. 86 (2003) 779–816. [CrossRef] [MathSciNet] [Google Scholar]
  6. T. Fliegner, H. Logemann and E.P. Ryan, Low-gain integral control of well-posed infinite-dimensional linear systems with input and output nonlinearities. J. Math. Anal. Appl. 261 (2001) 307–336. [CrossRef] [MathSciNet] [Google Scholar]
  7. R.B. Gorbet, K.A. Morris and W.L. Wang, Passivity-based stability and control of hysteresis in smart actuators. IEEE Trans. Control Systems Technology 9 (2001) 5–16. [Google Scholar]
  8. B.Z. Guo and Z.C. Shao, Regularity of a Schrödinger equation with Dirichlet control and colocated observation, Syst. Control Lett. 54 (2005) 1135–1142. [Google Scholar]
  9. B.Z. Guo and Z.C. Shao, Regularity of an Euler-Bernoulli plate with Neumann control and colocated observation, J. Dynam. Control Syst. 12 (2006) 405–418. [Google Scholar]
  10. B.Z. Guo and X. Zhang, The regularity of the wave equation with partial Dirichlet control and colocated observation, SIAM J. Control Optim. 44 (2005) 1598–1613. [Google Scholar]
  11. F. Ikhouane and J. Rodellar, A linear controller for hysteretic systems. IEEE Trans. Auto. Control 51 (2006) 340–344. [CrossRef] [Google Scholar]
  12. F. Ikhouane, V. Mañosa and J. Rodellar, Adaptive control of a hysteretic structural system. Automatica 41 (2005) 225–231. [CrossRef] [MathSciNet] [Google Scholar]
  13. U. Jönson, Stability of uncertain systems with hysteresis nonlinearities. Int. J. Robust Nonlinear Control 8 (1998) 279–293. [CrossRef] [Google Scholar]
  14. M.A. Krasnosel'skii and A.V. Pokrovskii, Systems with Hysteresis. Springer, Berlin (1989). [Google Scholar]
  15. I. Lasiecka and R. Triggiani, The operator 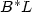Formula for the wave equation with Dirichlet control. Abstract Appl. Anal. 2004 (2004) 625–634. [CrossRef] [Google Scholar]
  16. H. Logemann and A.D. Mawby, Low-gain integral control of infinite-dimensional regular linear systems subject to input hysteresis, F. Colonius et al. Eds., Birkhäuser, Boston, Advances in Mathematical Systems Theory (2001) 255–293. [Google Scholar]
  17. H. Logemann and A. Mawby, Discrete-time and sampled-data low-gain integral control of infinite-dimensional linear systems in the presence of input hysteresis. SIAM J. Control Optim. 41 (2002) 113–140. [CrossRef] [MathSciNet] [Google Scholar]
  18. H. Logemann and E.P. Ryan, Time-varying and adaptive integral control of infinite-dimensional regular systems with input nonlinearities, SIAM J. Control Optim. 38 (2000) 1120–1144. [Google Scholar]
  19. H. Logemann and E.P. Ryan, Systems with hysteresis in the feedback loop: existence, regularity and asymptotic behaviour of solutions. ESAIM: COCV 9 (2003) 169–196. [EDP Sciences] [Google Scholar]
  20. H. Logemann, E.P. Ryan and S. Townley, Integral control of linear systems with actuator nonlinearities: lower bounds for the maximal regulating gain. IEEE Trans. Auto. Control 44 (1999) 1315–1319. [CrossRef] [Google Scholar]
  21. R. Rebarber and G. Weiss, Internal model based tracking and disturbance rejection for stable well-posed systems, Automatica 39 (2003) 1555–1569. [Google Scholar]
  22. D. Salamon, Control and Observation of Neutral Systems. Pitman, London (1984). [Google Scholar]
  23. D. Salamon, Infinite-dimensional linear systems with unbounded control and observation: a functional analytic approach. Trans. Amer. Math. Soc. 300 (1987) 383–431. [MathSciNet] [Google Scholar]
  24. O.J. Staffans, Well-Posed Linear Systems. Cambridge University Press, Cambridge (2005). [Google Scholar]
  25. O.J. Staffans and G. Weiss, Transfer functions of regular linear systems, part II: The system operator and the Lax-Phillips semigroup. Trans. Amer. Math. Soc. 354 (2002) 3229–3262. [CrossRef] [MathSciNet] [Google Scholar]
  26. X. Tan and J.S. Baras, Modeling and control of hysteresis in magnetostrictive actuators. Automatica 40 (2004) 1469–1480. [CrossRef] [MathSciNet] [Google Scholar]
  27. G. Tao and P.V. Kokotović, Adaptive Control of Systems with Actuator and Sensor Nonlinearities. John Wiley, (1996) [Google Scholar]
  28. M. Tucsnak and G. Weiss, How to get a conservative well-posed system out of thin air, part II: Controllability and stability. SIAM J. Control Optim. 42 (2003) 907–935. [CrossRef] [MathSciNet] [Google Scholar]
  29. G. Weiss, Transfer functions of regular linear systems, part I: Characterization of regularity. Trans. Amer. Math. Soc. 342 (1994) 827–854. [CrossRef] [MathSciNet] [Google Scholar]
  30. G. Weiss and R. Rebarber, Optimizability and estimatability for infinite-dimensional linear systems. SIAM J. Control Optim. 39 (2000) 1204–1232. [CrossRef] [MathSciNet] [Google Scholar]

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.