Free Access
| Issue |
ESAIM: COCV
Volume 14, Number 4, October-December 2008
|
|
|---|---|---|
| Page(s) | 802 - 824 | |
| DOI | https://doi.org/10.1051/cocv:2008011 | |
| Published online | 30 January 2008 | |
- B.A. Andreianov, M. Gutnic and P. Wittbold, Convergence of finite volume approximations for a nonlinear elliptic-parabolic problem: a “continuous" approach. SIAM J. Numer. Anal. 42 (2004) 228–251. [CrossRef] [MathSciNet] [Google Scholar]
- D.N. Arnold, An interior penalty finite element method with discontinuous elements. SIAM J. Numer. Anal. 19 (1982) 742–760. [CrossRef] [MathSciNet] [Google Scholar]
- D.N. Arnold, F. Brezzi, B. Cockburn and L.D. Marini, Unified analysis of discontinuous Galerkin methods for elliptic problems. SIAM J. Numer. Anal. 39 (2001-2002) 1749–1779. [Google Scholar]
- J.P. Aubin, Approximation des problèmes aux limites non homogènes pour des opérateurs non linéaires. J. Math. Anal. Appl. 30 (1970) 510–521. [CrossRef] [MathSciNet] [Google Scholar]
- I. Babuška, The finite element method with penalty. Math. Comp. 27 (1973) 221–228. [Google Scholar]
- I. Babuška and M. Zlámal, Nonconforming elements in the finite element method with penalty. SIAM J. Numer. Anal. 10 (1973) 863–875. [CrossRef] [MathSciNet] [Google Scholar]
- I. Babuška, C.E. Baumann and J.T. Oden, A discontinuous hp finite element method for diffusion problems: 1-D analysis. Comput. Math. Appl. 37 (1999) 103–122. [Google Scholar]
- C.E. Baumann and J.T. Oden, Advances and applications of discontinuous Galerkin methods in CFD. Computational mechanics (Buenos Aires, 1998), Centro Internac. Métodos Numér. Ing., Barcelona (1998). [Google Scholar]
- C.E. Baumann and J.T. Oden, A discontinuous hp finite element method for convection-diffusion problems. Comput. Methods Appl. Mech. Engrg. 175 (1999) 311–341. [CrossRef] [MathSciNet] [Google Scholar]
- C.E. Baumann and J.T. Oden, An adaptive-order discontinuous Galerkin method for the solution of the Euler equations of gas dynamics. Internat. J. Numer. Methods Engrg. 47 (2000) 61–73. [CrossRef] [MathSciNet] [Google Scholar]
- H. Brezis, Analyse fonctionnelle: Théorie et applications. Masson, Paris (1983). [Google Scholar]
- P.G. Ciarlet, The finite element method for elliptic problems. North Holland, Amsterdam (1978). [Google Scholar]
- P.G. Ciarlet, Basic error estimates for elliptic problems, in Handbook of numerical analysis, P.G. Ciarlet and J.-L. Lions Eds., North Holland, Amsterdam (1991). [Google Scholar]
- B. Cockburn and C.-W. Shu, The local discontinuous Galerkin method for time-dependent convection-diffusion systems. SIAM J. Numer. Anal. 35 (1998) 2440–2463. [CrossRef] [MathSciNet] [Google Scholar]
- B. Cockburn, G.E. Karniadakis and C.-W. Shu, The development of discontinuous Galerkin methods, in Discontinuous Galerkin methods (Newport, RI, 1999), Lect. Notes Comput. Sci. Eng. 11 (2000) 3–50. [Google Scholar]
- B. Dacorogna, Direct methods in the calculus of variations. Springer-Verlag, New York (1989). [Google Scholar]
- G. Dal Maso, An introduction to Γ-convergence. Birkäuser, Boston (1993). [Google Scholar]
- C. Davini, Piece-wise constant approximations in the membrane problem. Meccanica 38 (2003) 555–569. [CrossRef] [MathSciNet] [Google Scholar]
- C. Davini and F. Jourdan, Approximations of degree zero in the Poisson problem. Comm. Pure Appl. Anal. 4 (2005) 267–281. [CrossRef] [Google Scholar]
- C. Davini and R. Paroni, Generalized Hessian and external approximations in variational problems of second order. J. Elasticity 70 (2003) 149–174. [CrossRef] [MathSciNet] [Google Scholar]
- C. Davini and R. Paroni, Error estimate of piece-wise constant approximations to the Poisson problem (in preparation). [Google Scholar]
- C. Davini and I. Pitacco, Relaxed notions of curvature and a lumped strain method for elastic plates. SIAM J. Numer. Anal. 35 (1998) 677–691. [CrossRef] [MathSciNet] [Google Scholar]
- C. Davini and I. Pitacco, An unconstrained mixed method for the biharmonic problem. SIAM J. Numer. Anal. 38 (2000) 820–836. [CrossRef] [MathSciNet] [Google Scholar]
- L.C. Evans and R.F. Gariepy, Measure theory and fine properties of functions, Studies in Advanced Mathematics. CRC Press, Boca Raton (1992). [Google Scholar]
- J.-L. Lions, Problèmes aux limites non homogènes à données irrégulières : Une méthode d'approximation, in Numerical Analysis of Partial Differential Equations (C.I.M.E. 2 Ciclo, Ispra, 1967), Edizioni Cremonese, Rome (1968) 283–292. [Google Scholar]
-
J. Ne
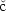 as, Équations aux dérivées partielles. Presses de l'Université de Montréal (1965).
[Google Scholar]
as, Équations aux dérivées partielles. Presses de l'Université de Montréal (1965).
[Google Scholar]
- J. Nitsche, Über ein Variationsprinzip zur Lösung von Dirichlet-Problemen bei Verwendung von Teilräumen, die keinen Randbedingungen unterworfen sind. Abh. Math. Sem. Univ. Hamburg 36 (1971) 9–15. [Google Scholar]
- W.H. Reed and T.R. Hill, Triangular mesh method for neutron transport equation. Tech. Report LA-UR-73-479, Los Alamos Scientific Laboratory, Los Alamos (1973). [Google Scholar]
- M.F. Wheeler, An elliptic collocation-finite element method with interior penalties. SIAM J. Numer. Anal. 15 (1978) 152–161. [CrossRef] [MathSciNet] [Google Scholar]
- X. Ye, A new discontinuous finite volume method for elliptic problems. SIAM J. Numer. Anal. 42 (2004) 1062–1072. [CrossRef] [MathSciNet] [Google Scholar]
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


