EDP Sciences logo
Subscriber Authentication Point
Search
Menu
All issues Volume 15 / No 3 (July-September 2009) ESAIM: COCV, 15 3 (2009) 653-675 References
Free Access
Issue
ESAIM: COCV
Volume 15, Number 3, July-September 2009
Page(s) 653 - 675
DOI https://doi.org/10.1051/cocv:2008055
Published online 20 August 2008
  1. A. Ambrosetti, M. Badiale and S. Cingolani, Semiclassical states of nonlinear Schrödinger equations. Arch. Ration. Mech. Anal. 140 (1997) 285–300. [CrossRef] [Google Scholar]
  2. A. Ambrosetti, A. Malchiodi and S. Secchi, Multiplicity results for some nonlinear Schrödinger equations with potentials. Arch. Ration. Mech. Anal. 159 (2001) 253–271. [CrossRef] [MathSciNet] [Google Scholar]
  3. G. Arioli and A. Szulkin, A semilinear Schrödinger equations in the presence of a magnetic field. Arch. Ration. Mech. Anal. 170 (2003) 277–295. [CrossRef] [MathSciNet] [Google Scholar]
  4. S. Barile, S. Cingolani and S. Secchi, Single-peaks for a magnetic Schrödinger equation with critical growth. Adv. Diff. Equations 11 (2006) 1135–1166. [Google Scholar]
  5. T. Bartsch, E.N. Dancer and S. Peng, On multi-bump semi-classical bound states of nonlinear Schrödinger equations with electromagnetic fields. Adv. Diff. Equations 11 (2006) 781–812. [Google Scholar]
  6. H. Berestycki and P.L. Lions, Nonlinear scalar field equation I. Arch. Ration. Mech. Anal. 82 (1983) 313–346. [Google Scholar]
  7. J. Byeon and L. Jeanjean, Standing waves for nonlinear Schrödinger equations with a general nonlinearity. Arch. Ration. Mech. Anal. 185 (2007) 185–200. [Google Scholar]
  8. J. Byeon and L. Jeanjean, Erratum: Standing waves for nonlinear Schrödinger equations with a general nonlinearity. Arch. Ration. Mech. Anal. DOI 10.1007/s00205-006-0019-3. [Google Scholar]
  9. J. Byeon and L. Jeanjean, Multi-peak standing waves for nonlinear Schrödinger equations with a general nonlinearity. Discrete Cont. Dyn. Systems 19 (2007) 255–269. [CrossRef] [Google Scholar]
  10. J. Byeon and Z.-Q. Wang, Standing waves with critical frequency for nonlinear Schrödinger equations. Arch. Rat. Mech. Anal. 165 (2002) 295–316. [CrossRef] [Google Scholar]
  11. J. Byeon and Z.-Q. Wang, Standing waves with critical frequency for nonlinear Schrödinger equations II. Calc. Var. Partial Differ. Equ. 18 (2003) 207–219. [CrossRef] [Google Scholar]
  12. J. Byeon, L. Jeanjean and K. Tanaka, Standing waves for nonlinear Schrödinger equations with a general nonlinearity: one and two dimensional cases. Comm. Partial Diff. Eq. 33 (2008) 1113–1136. [CrossRef] [Google Scholar]
  13. D. Cao and E.-S. Noussair, Multi-bump standing waves with a critical frequency for nonlinear Schrödinger equations. J. Diff. Eq. 203 (2004) 292–312. [Google Scholar]
  14. T. Cazenave, Semilinear Schrödinger equations, Courant Lecture Notes. AMS (2003). [Google Scholar]
  15. J. Chabrowski and A. Szulkin, On the Schrödinger equation involving a critical Sobolev exponent and magnetic field. Topol. Methods Nonlinear Anal. 25 (2005) 3–21. [MathSciNet] [Google Scholar]
  16. S. Cingolani, Semiclassical stationary states of nonlinear Schrödinger equations with an external magnetic field. J. Diff. Eq. 188 (2003) 52–79. [CrossRef] [Google Scholar]
  17. S. Cingolani and M. Lazzo, Multiple positive solutions to nonlinear Schrödinger equations with competing potential functions. J. Diff. Eq. 160 (2000) 118–138. [Google Scholar]
  18. S. Cingolani and M. Nolasco, Multi-peaks periodic semiclassical states for a class of nonlinear Schrödinger equations. Proc. Royal Soc. Edinburgh 128 (1998) 1249–1260. [Google Scholar]
  19. S. Cingolani and S. Secchi, Semiclassical limit for nonlinear Schrödinger equations with electromagnetic fields. J. Math. Anal. Appl. 275 (2002) 108–130. [CrossRef] [MathSciNet] [Google Scholar]
  20. S. Cingolani and S. Secchi, Semiclassical states for NLS equations with magnetic potentials having polynomial growths. J. Math. Phys. 46 (2005) 1–19. [Google Scholar]
  21. M. Clapp, R. Iturriaga and A. Szulkin, Periodic solutions to a nonlinear Schrödinger equations with periodic magnetic field. Preprint. [Google Scholar]
  22. V. Coti-Zelati and P.H. Rabinowitz, Homoclinic orbits for second order Hamiltonian systems possessing superquadratic potentials. J. Amer. Math. Soc. 4 (1991) 693–727. [CrossRef] [MathSciNet] [Google Scholar]
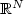  23. V. Coti-Zelati and P.H. Rabinowitz, Homoclinic type solutions for a semilinear elliptic PDE on Formula . Comm. Pure Appl. Math. 45 (1992) 1217–1269. [CrossRef] [MathSciNet] [Google Scholar]
  24. M. Del Pino and P. Felmer, Local mountain passes for semilinear elliptic problems in unbounded domains. Calc. Var. Partial Differ. Equ. 4 (1996) 121–137. [CrossRef] [MathSciNet] [Google Scholar]
  25. M. Del Pino and P. Felmer, Semi-classical states for nonlinear Schrödinger equations. J. Funct. Anal. 149 (1997) 245–265. [CrossRef] [MathSciNet] [Google Scholar]
  26. M. Del Pino and P. Felmer, Multi-peak bound states for nonlinear Schrödinger equations. Ann. Inst. H. Poincaré Anal. Non Linéaire 15 (1998) 127–149. [CrossRef] [MathSciNet] [Google Scholar]
  27. M.J. Esteban and P.L. Lions, Stationary solutions of nonlinear Schrödinger equations with an external magnetic field, in PDE and Calculus of Variations, in honor of E. De Giorgi, Birkhäuser (1990). [Google Scholar]
  28. A. Floer and A. Weinstein, Nonspreading wave packets for the cubic Schrödinger equation with a bounded potential. J. Funct. Anal. 69 (1986) 397–408. [CrossRef] [MathSciNet] [Google Scholar]
  29. D. Gilbarg and N.S. Trudinger, Elliptic Partial Differential Equations of Second Order, second edition, Grundlehren 224. Springer, Berlin, Heidelberg, New York and Tokyo (1983). [Google Scholar]
  30. C. Gui, Existence of multi-bump solutions for nonlinear Schrödinger equations. Comm. Partial Diff. Eq. 21 (1996) 787–820. [CrossRef] [Google Scholar]
  31. H. Hajaiej and C.A. Stuart, On the variational approach to the stability of standing waves for the nonlinear Schrödinger equation. Advances Nonlinear Studies 4 (2004) 469–501. [Google Scholar]
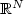  32. L. Jeanjean and K. Tanaka, A remark on least energy solutions in Formula . Proc. Amer. Math. Soc. 131 (2003) 2399–2408. [CrossRef] [MathSciNet] [Google Scholar]
  33. L. Jeanjean and K. Tanaka, A note on a mountain pass characterization of least energy solutions. Advances Nonlinear Studies 3 (2003) 461–471. [Google Scholar]
  34. L. Jeanjean and K. Tanaka, Singularly perturbed elliptic problems with superlinear or asympotically linear nonlinearities. Calc. Var. Partial Diff. Equ. 21 (2004) 287–318. [Google Scholar]
  35. K. Kurata, Existence and semi-classical limit of the least energy solution to a nonlinear Schrödinger equation with electromagnetic fields. Nonlinear Anal. 41 (2000) 763–778. [Google Scholar]
  36. Y.Y. Li, On a singularly perturbed elliptic equation. Adv. Diff. Equations 2 (1997) 955–980. [Google Scholar]
  37. P.L. Lions, The concentration-compactness principle in the calculus of variations. The locally compact case. Part II. Ann. Inst. H. Poincaré Anal. Non Linéaire 1 (1984) 223–283. [Google Scholar]
  38. Y.G. Oh, Existence of semiclassical bound states of nonlinear Schrödinger equations. Comm. Partial Diff. Eq. 13 (1988) 1499–1519. [CrossRef] [Google Scholar]
  39. M.H. Protter and H.F. Weinberger, Maximum Principles in Differential Equations. Springer-Verlag, New York, Berlin, Heidelberg and Tokyo (1984). [Google Scholar]
  40. P. Rabinowitz, On a class of nonlinear Schrödinger equations. Z. Angew. Math. Phys. 43 (1992) 270–291. [Google Scholar]
  41. M. Reed and B. Simon, Methods of Modern Mathematical Physics, Vol. II. Academic press, New York (1972). [Google Scholar]
  42. S. Secchi and M. Squassina, On the location of spikes for the Schrödinger equations with electromagnetic field. Commun. Contemp. Math. 7 (2005) 251–268. [CrossRef] [MathSciNet] [Google Scholar]
  43. W. Strauss, Existence of solitary waves in higher dimensions. Comm. Math. Phys. 55 (1977) 149–162. [CrossRef] [MathSciNet] [Google Scholar]
  44. M. Struwe, Variational Methods, Application to Nonlinear Partial Differential Equations and Hamiltonian Systems. Springer-Verlag (1990). [Google Scholar]
  45. X. Wang and B. Zeng, On concentration of positive bound states of nonlinear Schrödinger equation with competing potential functions. SIAM J. Math. Anal. 28 (1997) 633–655. [CrossRef] [MathSciNet] [Google Scholar]

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.