EDP Sciences logo
Subscriber Authentication Point
Search
Menu
All issues Volume 15 / No 4 (October-December 2009) ESAIM: COCV, 15 4 (2009) 895-913 References
Free Access
Issue
ESAIM: COCV
Volume 15, Number 4, October-December 2009
Page(s) 895 - 913
DOI https://doi.org/10.1051/cocv:2008056
Published online 20 August 2008
  1. D. Applegate, R. Bixby, V. Chavátal and W. Cook, On the solution of traveling salesman problems, in Doc. Math., Extra volume ICM 1998 III, Berlin (1998) 645–656. [Google Scholar]
  2. S. Arora, Polynomial time approximation schemes for Euclidean traveling salesman and other geometric problems. J. ACM 45 (1998) 753–782. [CrossRef] [MathSciNet] [Google Scholar]
  3. S. Arora, Approximation schemes for NP-hard geometric optimization problems: a survey. Math. Program. 97 (2003) 43–69. [MathSciNet] [Google Scholar]
  4. S. Arora, P. Raghavan and S. Rao, Approximation schemes for Euclidean k-medians and related problems, in ACM Symposium on Theory of Computing (1998) 106–113. [Google Scholar]
  5. H. Attouch and R.J.-B. Wets, Quantitative stability of variational systems: I. The epigraphical distance. Trans. Amer. Math. Soc. 328 (1991) 695–729. [CrossRef] [MathSciNet] [Google Scholar]
  6. H. Attouch and R.J.-B. Wets, Quantitative stability of variational systems: II. A framework for nonlinear conditioning. SIAM J. Optim. 3 (1993) 359–381. [CrossRef] [MathSciNet] [Google Scholar]
  7. S. Äyrämö, Knowledge Mining Using Robust Clustering. Jyväskylä Studies in Computing 63. University of Jyväskylä, Ph.D. thesis (2006). [Google Scholar]
  8. J.J. Bentley, Fast algorithms for geometric traveling salesman problems. ORSA J. Comput. 4 (1992) 887–411. [Google Scholar]
  9. G. Buttazzo and E. Stepanov, Minimization problems for average distance functionals, in Calculus of Variations: Topics from the Mathematical Heritage of Ennio De Giorgi, D. Pallara Ed., Quaderni di Matematica, Seconda Università di Napoli, Caserta 14 (2004) 47–83. [Google Scholar]
  10. K. Helsgaun, An effective implementation of the Lin-Kernighan traveling salesman heuristic. Eur. J. Oper. Res. 126 (2000) 106–130. [CrossRef] [Google Scholar]
  11. J.-B. Hiriart-Urruty and C. Lemaréchal, Convex analysis and minimization algorithms I-II. Springer (1993). [Google Scholar]
  12. R. Horst and P.M. Pardolos Eds., Handbook of Global Optimization. Kluwer Academic Publishers (1995). [Google Scholar]
  13. D.S. Johnson and L.A. McGeoch, The traveling salesman problem: A case study in local optimization, in Local Search in Combinatorial Optimization, E. Aarts and J. Lenstra Eds., John Wiley and Sons (1997) 215–310. [Google Scholar]
  14. D.S. Johnson and L.A. McGeoch, Experimental analysis of heuristics for the STSP, in The Traveling Salesman Problem and Its Variations, G. Gutin and A.P. Punnen Eds., Springer (2002) 369–443. [Google Scholar]
  15. J.D. Litke, An improved solution to the traveling salesman problem with thousands of nodes. Commun. ACM 27 (1984) 1227–1236. [CrossRef] [Google Scholar]
  16. D.S. Mitrinović, Analytic Inequalities. Springer-Verlag (1970). [Google Scholar]
  17. S. Peyton Jones, Haskell 98 Language and Libraries: The Revised Report. Cambridge University Press (2003). [Google Scholar]
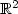  18. P. Polak and G. Wolansky, The lazy travelling salesman problem in Formula . ESAIM: COCV 13 (2007) 538–552. [CrossRef] [EDP Sciences] [Google Scholar]
  19. G. Reinelt, TSPLIB – A traveling salesman problem library. ORSA J. Comput. 3 (1991) 376–384. [Google Scholar]
  20. R.T. Rockafellar, Convex Analysis. Princeton University Press (1972). [Google Scholar]
  21. R.T. Rockafellar and R.J.-B. Wets, Variational Analysis. Springer (1998). [Google Scholar]
  22. T. Valkonen, Convergence of a SOR-Weiszfeld type algorithm for incomplete data sets. Numer. Funct. Anal. Optim. 27 (2006) 931–952. [CrossRef] [MathSciNet] [Google Scholar]
  23. T. Valkonen and T. Kärkkäinen, Clustering and the perturbed spatial median. Computer and Mathematical Modelling (submitted). [Google Scholar]

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.